Amplification and decoherence

Thus far, we have shown many examples of two particles interacting and blithely called those interactions “measurements” (or to be more careful “micromeasurements”). We have let the question linger: do these effects that we see for individual particles still happen when we are considering many, many particles? For example, do the many, many particles making up a laboratory measurement device also exhibit the properties of entangled states we have seen so far? Even more unsettling is to ask whether the many, many particles in our brains — those responsible for generating our consciousness — follow the same rules.

This is the question underlying the Schrödinger’s cat thought experiment. The cat is in a box with a device that takes a microscopic quantum process, such as decay of a radioactive atom, and somehow turns that into a macroscopic effect. Specifically, releasing (or not) a poison that kills (or does not kill) the cat. Typical questions are whether the cat is alive, dead or somehow both at once, and whether our opening of the box and observing of the cat makes a difference.

We will argue here that, at a fundamental level, it is plausible to say that indeed complex macroscopic systems follow the same quantum rules that govern a few microscopic particles. The differences are really a matter of degree, as opposed to a matter of kind. The main issue relates to complementary observables. Recall that we saw that when a micromeasurement is performed, information about a complementary observable is not lost, but it becomes more difficult to obtain. (That is, it becomes more difficult for that information to be transferred to another system.) We will see that if many particles become involved in a measurement, then that information about the complementary observable becomes really, really hard to obtain. So much so, that we could say it is effectively impossible. This is the idea of decoherence.

A measurement device

In the spirit of this tutorial, let’s try to come up with a physically plausible way to take the result of a micromeasurement and turn it into a macroscopic measurement that we could see with our own eyes. But first let’s acknowledge that it’s actually pretty hard, in practice, to build an apparatus to accomplish this. This is why, despite Einstein and others proposing thought experiments in the 1930s, and Bell proposing his test of quantum theory in the 1960s, we didn’t get the first actual experiment along these lines until the 1970s. And it hasn’t been until the last couple of decades that we have figured out how to perform this trick well enough to start building rudimentary quantum computers. So you can’t expect any old system to be able to amplify a single micromeasurement up to the macro scale – it’s going to take some serious engineering.

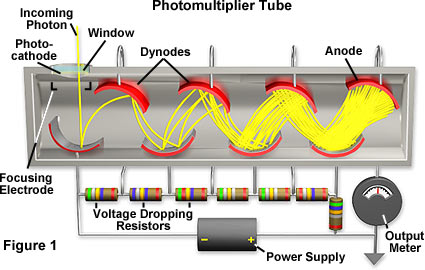
But the practical difficulties don’t need to stop us from proposing an idea that we can simulate. In fact, our idea is a simplified picture of just the kind of detector used by Clauser and Freedman in their 1972 experiment testing Bell’s theory: a photomultiplier. A photomultiplier is commonly used as a detector for photons, though as we will see, the first step is to convert the photon into an electron, so one could easily use the same idea to detect an electron directly.

The idea behind a photomultiplier is that you start with one electron, then amplify that electron into multiple electrons, and then repeat that amplification a number of times until you get a macroscopically measurable electrical signal. A diagram of a photomultiplier is shown in Fig. 8.1. An incoming photon is absorbed by the photocathode, which then emits an electron. That electron hits the first dynode, which is a curved piece of metal held at some voltage. The impact of the electron with the dynode knocks some electrons loose from the metal. Because the next dynode is held at a higher voltage, there is an electric field that accelerates the electrons from one dynode to the next. When the electrons hit the next dynode with higher energy, they each free multiple additional electrons. This process is repeated until there are enough electrons to yield a measurable electrical current flowing into the anode. We’ll try to follow this general idea and see how it works.

Figure 8.1

Diagram of a photomultiplier, courtesy of Hamamatsu, a manufacturer of photomultipliers.

First, let’s try to build a measurement device to distinguish between two possible positions of an electron. The first step will be to separate the two positions, and accelerate the electron in either direction. This could be accomplished by placing a heavy charged particle right between the two positions that repels our electron. If the electron is on one side, it will be accelerated away in one direction, and accelerated away in the other direction on the other side. This new particle is heavy enough that it doesn’t recoil significantly, and therefore doesn’t become entangled with our electron. This means we might as well replace this heavy particle with an external potential as shown by the gray line in Fig. 8.2. Here we show an initial electron state as a superposition of packets in two positions. But we can easily imagine what it would look like with a packet just on one side or the other. The electron essentially rolls downhill in either direction. We can see that the particle is gaining speed and energy by seeing the packets’ motion speed up, and also by the shortening wavelength.

Figure 8.2

Video example of initial separation and acceleration of a proposed measurement device.

The next part of the plan is that our fast moving electron will knock into a heavier particle pre-positioned on either side, sending that heavier particle off in the same direction as the particle that hit it. We can put the heavier particle in a well so that it stays put while waiting to be hit. This is somewhat different than the photomultiplier, where instead of launching a single heavier particle, multiple identical particles are launched from each dynode. But we will stick with a single heavier particle, since visualization becomes more difficult as we increase the number of particles, and also because in our fictional device we don’t have to accept the limited menu of particles offered by nature.

A simulation of this process is shown in Fig. 8.3 [1]. Particle 1 is initially a single wave packet traveling to the left. Particle 2, which is twice as heavy, is initially in the lowest-frequency confined wave in a well centered at \(x=0\). The boundaries of the well are indicated by the green dotted lines. The range over which particle 1 and 2 repel each other is set to be the same as the well width, so they start repelling before particle 1 has entered the well. Before the collision, we see that particle 2 is confined to the well by the fact that the blob does not change in the vertical direction. After the collision, we see that the blob is now moving diagonally towards the lower right. This indicates that particle 1 has recoiled back in the positive \(x\) direction, and particle 2 has left the well, now traveling towards more negative \(x\). Particle 2 is moving more slowly than particle 1 because it is heavier.

Figure 8.3

Video example of the accelerated wave packet knocking a heavier particle out of a well and recoiling. The well boundaries are indicated by the green dotted lines.

Now the idea is that we just chain together the same thing multiple times, as shown in Fig. 8.4. Accelerate a particle, and have it knock loose a heavier particle. Then accelerate that heavier particle, and have it knock loose a still heavier particle. We can repeat this as many times as needed to get the particle to be large enough that we can see it by eye. For example, the initial electron hits a proton, the proton hits an atom, the atom hits a small molecule, the small molecule hits a protein, the protein hits a virus, the virus hits a bacterium, the bacterium hits a speck of dust, the speck of dust hits a grain of sand, the grain of sand hits a small ball bearing, the ball bearing hits a marble [2]. By the end, this starts to resemble a “marble run” toy, or a Rube Goldberg machine, with each heavier particle balanced in a little divot from which it gets knocked free. At last, the marble hits a lever that causes a pointer to rotate. This last marble is labeled “L” and “R” on the two sides, and when it rolls down the last ramp it will push the bottom part of the pointer so it rotates to point at “left” or “right”.

Figure 8.4

Schematic for a “marble run” device that amplifies the outcome of a micromeasurement into a macroscopic measurement of position.

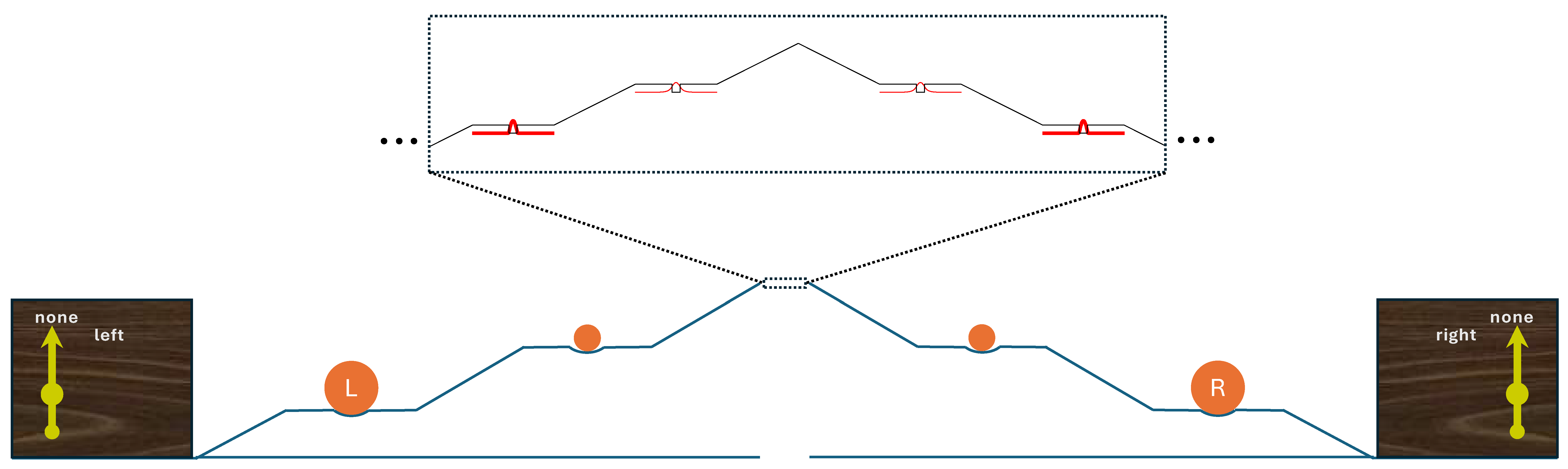
It is pretty clear that if we start a wave packet on the left side of the central peak in Fig. 8.2 (or in the inset of Fig. 8.4), the final state will be one where the left pointer is pointing to the label “left.” Let’s try to picture this process as a multi-particle wave function. The pointer on the left is initially in the state \(|\mathrm{none}_L\rangle\). First, the initial packet collides with the first confined particle. This is what was shown in Fig. 8.3, resulting in a single blob going off at some angle in the 2D plot. This blob is correlated with the pointer state \(|\mathrm{none}_L\rangle\). The heavier particle then accelerates down the ramp. (Who knows what happens to the original particle. It might wind up bouncing off the up-ramp and eventually coming down the ramp too, or maybe gets partially stuck in the well.) When the heavier particle collides with the still heavier particle after it, we should consider this new particle in the wave function also. Now we have a 3D plot, where the blob will go off at some angle as the new particle is kicked out of its well. The same thing happens each time the next particle is kicked out: we add another dimension to the plot, but we still just have a single blob. Finally, the last marble has been knocked out and we still have a single blob, now in many-dimensional space. This hyperblob is still correlated with the pointer state \(|\mathrm{none}_L\rangle\). The interaction between the marble and the pointer then causes the pointer state to rotate to \(|\mathrm{left}\rangle\). The blob is now correlated with the pointer state \(|\mathrm{left}\rangle\).

Clearly, we could go through the exact same description for the initial particle starting on the right side, resulting in a blob representing all the particles in the right chain being knocked free, ultimately correlated with the other pointer in the state \(|\mathrm{right}\rangle\).

But what if we start the initial particle in a superposition of the two positions, as shown in Fig. 8.2? Everything should stay the same, except now we have two blobs. The pointers start in the states \(|\mathrm{none}_L\rangle\) and \(|\mathrm{none}_R\rangle\). As soon as the initial particle knocks out the first particles in the left and right chains, the two packets become entangled with two different particles, represented as two misaligned blobs. Visualized as a 3D plot, the two blobs, separated in the \(x_1\) direction, start out aligned in the \(x_2\), and \(x_3\) directions. When the packet on the left interacts with one particle and the packet on the right interacts with the other particle, one blob veers off in the \(x_2\) direction, and the other veers off in the \(x_3\) direction. As they subsequently interact with more particles on the two sides, the two blobs keep veering off into different directions from each other. Ultimately, one blob represents all the particles on the left and becomes correlated with the pointer state \(|\mathrm{left}\rangle\) and the other blob, representing all the particles on the right becomes correlated with the pointer state \(|\mathrm{right}\rangle\).

So in the end, we have a state where the left pointer is pointing to “left” and also, the pointer on the right is pointing to “right”, but each outcome is correlated with a different component of an entangled state of many particles. The strangeness of this situation might be better appreciated if we have just a single pointer. Imagine that the “marble run” track shown in Fig. 8.4 curves around so the two ends wind up meeting at the same place. Now we can have a pointer with three positions as shown in Fig 8.5. This doesn’t materially change the description at all. If we start a wave packet only on the left side, we get a blob correlated with the pointer state \(|\mathrm{left}\rangle\), and the same on the right. If we start with a superposition of two packets on the left and right, we end up with one blob correlated with \(|\mathrm{left}\rangle\) and another blob correlated with \(|\mathrm{right}\rangle\). This is a situation where the macroscopic pointer is simultaneously pointing to the left and the right.

Figure 8.5

Modification to the measurement devices in Fig 8.4 where the two ends wrap around to meet at a single pointer device.

The scenario described above, where a macroscopic object (the pointer) is simultaneously in two very different states, is not at all what we are used to. Is this really possible? It seems crazy, but at the same time, it seems to be what the Schrödinger equation predicts. It is the position of the Many Worlds, or Everett, interpretation that this does indeed happen. In a later section, we will discuss how such a result can be reconciled with our everyday experience that such things do not happen. But first, let’s look at this behavior a little more carefully.

In the version of the measurement device shown in Fig 8.5, we see that if the initial wave function is a superposition of both sides then the two marbles “L” and “R” meet in the middle. What happens when they cross? Do they collide? The answer is no! At the moment when the two marbles are heading towards each other, recall that the state is represented by two blobs. One represents the particles in the left path being knocked out and the particles in the right path remaining at rest. The other blob represents the opposite — the particles in the right path being knocked out and the particles in the left path remaining at rest. So just looking at the blob that represents the particles moving in the left path, when the “L” marble reaches the pointer, the “R” marble is still sitting in its divot. For the other blob, the “L” marble is still sitting in its divot when the “R” marble reaches the pointer. Thus neither blob approaches the dividing plane where the “L” marble and “R” marble coordinates become equal, and so the two marbles do not collide at the pointer. They will only collide if the “L” marble is able to make it up the right ramp to reach the stationary “R” marble, and vice versa.

A wave function in this type of situation is illustrated in Fig. 8.6. The top panel shows the initial non-entangled setup. Particle 2 is separated into a superposition of two packets each heading inwards. Two particles (Particle 1 and 3) sit at rest in between the components of particle 2. The particles will interact as usual so that the left packet of particle 2 will collide with particle 1, and the right packet will collide with particle 3.

Figure 8.6

Illustration of a three particle wave function where two components of particle 2 each collide with separate particles, particle 1 and 3, which are initially at rest. Top panel shows the initial unentangled separate wave functions. Green blobs in the lower panel show the initial three-particle wave function, with arrows indicating how the blobs will move.

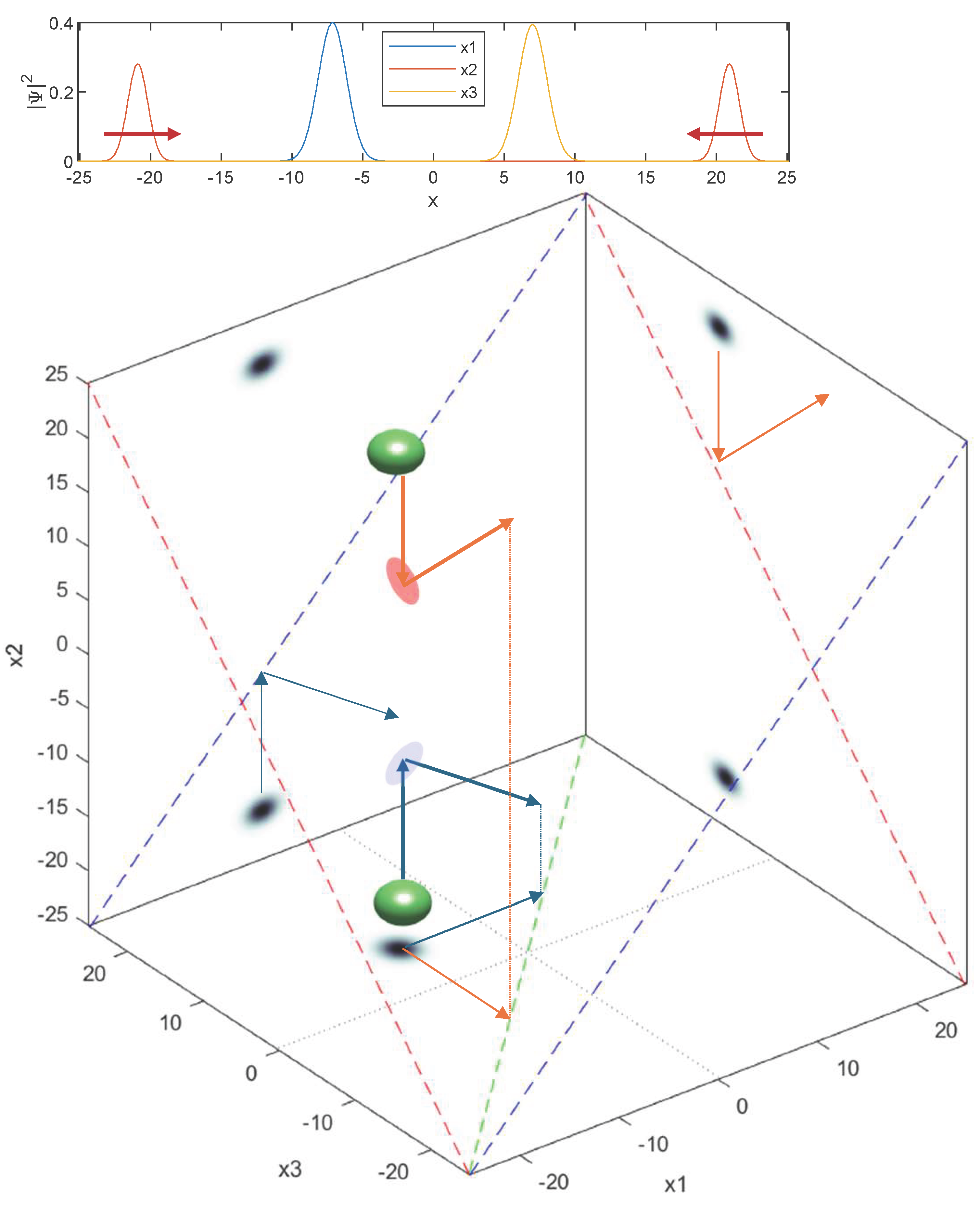
To understand how the system evolves in time, we had better look at the three-particle wave function shown in the bottom panel of Fig. 8.6. There are initially two blobs moving towards each other in the vertical \(x_2\) direction, corresponding to the two packets of particle 2. Both blobs are in the same \(x_1\) and \(x_3\) positions, due to the single packets for particle 1 and 3. When the blobs reach the point where \(x_2 = x_1\) (on the blue diagonal plane) and where \(x_2=x_3\) (on the red diagonal plane), the two particle 2 packets collide with particles 1 and 3. The top blob represents the collision with particle 3 and deflects in the \(x_3\) direction. The bottom blob represents the collision with particle 1 and deflects in the \(x_1\) direction.

The arrows on the bottom plane of Fig. 8.6 show the blob trajectories after the collision. We can see that there is a moment when the top blob has \(x_3 = 0\) and the bottom blob has \(x_1 = 0\) (see the dotted lines on the bottom plane indicating these positions). So in some sense, components of both particles are crossing at \(x = 0\). This is like marble “L” and “R” both arriving at the pointer at the same time. However, these are on well-separated blobs, so they do not interact. The interaction between particles 1 and 3 only occurs when either blob reaches the plane indicated by the green dashed line, where \(x_1 = x_3\). This happens when the deflected component of particle 1 reaches the stationary component of particle 3 with which it is correlated, and vice versa. We really have to imagine two separate scenarios occurring simultaneously, yet independently: particle 1 being launched and eventually colliding with the stationary particle 3, and particle 3 being launched and eventually colliding wth the stationary particle 1. The fact that some parts of these two scenarios may at times overlap spatially is irrelevant.

It seems strange that somehow both marbles are simultaneously arriving at the pointer (and deflecting the pointer one way or the other), but they don’t collide. It seems like they just pass right through each other and leave the pointer simultaneously pointing in two directions. It might make it more clear if we imagine the two scenarios existing in two separate worlds. One world where the particle is measured to be on the left and one where it is measured to be on the right.

Decoherence

But we previously found that we have to careful about declaring separate blobs to be in separate worlds — sometimes the two worlds can come back together. For example, we saw in the Quantum Eraser section that if we measure a complementary observable on the measurement device itself, we can restore the interference seen in the original particle. Would it be possible, after the whole measurement process, to go back and obtain interference between the two components of the original wave packet?

As before, the way to bring back the interference would be to bring the blobs back into alignment somehow, so that when the two packets of the original particle cross, the blobs themselves overlap. Now it is much harder though, because each packet became entangled with a whole bunch of other particles in the chain from micro to macro. We would have realign the blobs in each dimension corresponding to each particle. As before, we could try to do a complementary measurement on each of them. Since what our measurement device measures is essentially “which path” information, we want to measure the phase difference between packets to “erase” that information.

Starting from the original particle in a superposition of left and right packets, each particle along the chain winds up in a superposition of two components: one where it is knocked free (correlated with all the other particles on that side knocked free), and another where it remains at rest (correlated with all the other particles on that side at rest.) We would need to somehow get those two components to cross, and position an atom phase sensor at the crossing point. Then we get the behavior seen in the Quantum Eraser section, where that particle splits up into symmetric pairs of packets that restore the alignment of the blobs in that dimension. So as long as we can do this for all of the particles in the chain, we should wind up with basically a many-dimensional grid (a hypercube) of blobs. Then if the packets of the original particle cross, those blobs will all overlap with their partner and interference will occur.

But there is a further problem with the idea above for restoring the interference after a macroscopic position measurement. One clue to this problem is that it might seem a bit strange to think about performing a measurement of the phase between interfering components of a marble. That’s just not something that a marble (or any macroscopic object) does.

The problem lies in the fact that as the particles become larger, there is a much greater chance of unintentional interactions with other particles, like air molecules or photons. It’s really pretty hard to avoid for a macroscopic object. We might be able to avoid it for a microscopic system. For example, it’s possible to protect some atoms by trapping them within a well-shielded ultra-high vacuum chamber. This is what is done in so-called ion-trap quantum computers. But at some point, the information has to be transferred to something larger, whether it is a pointer moving on a dial, or a large number of electrons in a wire.

There are two ways that unintentional interactions with other particles could cause problems. The first is simply that a collision physically knocks something off course. For example, in our proposed measurement device, if an air molecule collided with one of the smaller particles, it might knock it off course enough that it fails to hit the next particle in the chain. This would cause the measurement to fail. This will be more of an issue for the smaller particles, and so we need to carefully shield those particles. This might be difficult, but it is conceivable.

But the other problem is even more pernicious. This is that an interaction could cause one of the particles in the chain to become unintentionally entangled with an external particle. The reason why this is such a problem is that a collision between the large particle with a very small particle might barely move the large particle, but still cause the two to become fully entangled. For example, imagine our final marble in a superposition of having been knocked loose, and still remaining in its divot. If any particle, such as an air molecule, bounces off one component of the marble (and thus does not bounce off the other spatially separated component), this results in an entangled state between the marble and the air molecule. One of the blobs now gets sent off along a new dimension, corresponding to the motion of the air molecule.

Entanglement of a heavy particle in two distinct positions with a much lighter particle is simulated in Fig. 8.7. Particle 1, shown along the horizontal axis is 200 times heavier than particle 2, shown along the vertical axis. Somewhat perversely, the heavier particle has a much narrower wave packet in the simulation. It turns out that making heavier particles narrower greatly simplifies the simulation method. But the widths of the packets are not the important factors here, just the masses. The heavy particle is initially in a superposition of two packets at \(x=0\) and \(x=10\), and the light particle is a single wave packet. The light particle is moving much faster than the heavy particle, and the packets collide when they reach the same position at the white dotted line. We see that the light particle bounces right off the heavy particle (reversing direction on the vertical axis) without any noticeable change in the heavy particle’s position (staying put on the horizontal axis). Nonetheless, the two particles become unambiguously entangled. If you then applied some force to move the two heavy packets past each other, they would not interfere, as the blobs would not overlap.

Figure 8.7

Video example of a heavy particle (particle 1), initially in a superposition of two wave packets, becoming entangled via a collision with a much lighter particle (particle 2, 200x lighter).

In the simulation in Fig. 8.7, we can imagine that the heavy particle 1 is a marble, and the light particle 2 is an air molecule. In that case, not only would particle 1 be much heavier than particle 2, it would also be much bigger. This would provide an even larger target for air molecules to hit. So we can imagine that this process will happen very quickly. All it takes is a single air molecule colliding with the marble to completely misalign the blobs, and preclude interference between the components of the marble.

Now if we want to realign the blobs and restore interference between the original packets of the initial particle, we have to track down that pesky air molecule, and perform a phase measurement on it too! As you can see, the problem is that many, many particles are going to be bouncing off of the marble. There is no way we can track down all of them (or probably any of them) and hope to perform a complementary measurement on them.

This is why we don’t see interference for macroscopic objects. As the object gets bigger, there are more and more unintentional entanglements with particles in the environment. There is no hope of ever undoing them, to the extent that we can very safely say that any phase information between two macroscopic components is lost forever. In the wave function picture, a superposition of two distinct positions of a macroscopic object very rapidly become misaligned along many, many dimensions as particles in the environment bounce off of them. This is the process of decoherence.

Another way of looking at this is to imagine what would happen if we tried to amplify a phase micromeasurement in a similar way. It is not clear how one would go about this, but imagine we have some way of crossing two packets of a particle so that the interference transfers the phase information to the phase difference between the two packets of a larger particle. We could chain this process together until the particle’s interference was large enough to observe. Of course, this doesn’t work because as soon as any particle in the environment becomes entangled with one of the increasingly large particles in the measurement device, those two blobs become misaligned and can no longer interfere, thereby causing the measurement to fail.

We have seen how the environment singles out one particular quantity out of a set of complementary observables that we can measure. Ultimately, the observable that we can measure macroscopically is usually position. This is because most interactions that we can imagine depend on position, so any complementary quantities that do not have well-defined position will quickly become entangled with the environment once the system becomes large enough. That means that if we want to measure some microscopic observable, we usually want to to translate that information into position information before amplifying it.

For example, here is one idea for amplifying a phase micromeasurement. We saw back in the Complementary observables section, that our “atom” phase sensor works by switching between two different confined waves, the \(|+\rangle\) and \(|-\rangle\) states. Looking back at Fig. 5.2, we recall that, in that example, one of those waves is localized mainly on the left of the well, and the other on the right side of the well. So actually, we have already translated the information about the phase difference between the wave packets to a position of the wave in the well. Now we just need to somehow release the particle from the well, and perform the position measurement as outlined above. Perhaps we can somehow add some energy to the particle in the well so it can escape, and we can bring in a heavy charged particle right between the \(|+\rangle\) and \(|-\rangle\) waves to send them off in different directions.

In practice, we might not even bother devising a separate complementary micromeasurement if we can just manipulate the initial state so as to translate the information we want into a form that can be measured by the practically easiest micromeasurement. This is what is done in most actual quantum devices: we go to a lot of trouble to make one really nice measurement of one observable, then manipulate the state before measurement to get the desired information. That is hard enough, without trying to figure out how to do multiple different types of measurements.

In our example, we can translate between phase and position information with a beam splitter. We have seen how a beam splitter can translate a packet with well-defined position into one with well-defined phase difference. The opposite process also works — if we carefully combine two packets on a beam splitter we can get them to recombine into one packet, with the phase difference setting which way the resulting single packet goes. Note that this process does not constitute a phase micromeasurement, since, if we assume the beam splitter is heavy enough to not recoil significantly, the information about the phase has not been transferred to another system. (The situation would become tricky if this beam splitter were light enough to recoil, as we want it to be in a very precise position so as to translate the phase information reliably.) But now that we have changed the state so that what was phase information is now encoded as position information, we could then do our usual position micromeasurement to find out what the phase information was. We are still free then to send the particle back through a beam splitter if we want, to restore it to its original state (though now entangled with the position micromeasurement).

We are actually being a little bit sneaky here, because this is really what our atom phase micromeasurement is doing: when we overlap two packets to obtain interference we are translating the phase information into position information via the position of the interference fringes. Since the interaction between the wave packets and the atom depends on position (the overlap with the atom position), we can then transfer that once-phase/now-position information to the atom state. The packets then continue onwards, separating again thus returning to their original state of well-defined phase and not well-defined position.

In this and previous sections, we have now seen examples of quantum systems that display quantum measurement effects, without the need for asserting these effects axiomatically. In review, we have seen:

1. A measurement can distinguish between a set of distinct (technically orthogonal) states, such as well-separated positions. Other states, such as in-phase or out-of-phase linear combinations of those states, cannot be distinguished by the same measurement.

2. Unlike the standard measurement axiom, the measurement does not cause the state to collapse into one of the distinct states. However, a macroscopic measurement does result in very well separated blobs, corresponding to the different possible distinct states.

3. Once a measurement has distinguished between different orthogonal states, a repeated measurement of the same observable will yield correlation between repeated results.

4. Once a macroscopic measurement has distinguished between different orthogonal states, information about the complementary observables is effectively unobtainable, as it is now spread through many particles in the environment through the process of decoherence. Subsequent measurement of these observables would yield equal correlation of any possible outcomes with the results of the first measurement.

These observations replicate most of what the measurement axiom is needed for. There is one more piece of the measurement axiom, however. This piece specifies the probabilities with which different outcomes occur. This is a rather tricky aspect, so we will save it for the very last section. But first, we will next discuss in more detail what we have been alluding to about the whole “many worlds” business.

Footnotes

[1]

The simulation in Fig. 8.3 is lower resolution that the others shown here because situations like this are considerably more difficult to simulate. Specifically, simulating two interacting particles in an asymmetric situation rapidly becomes very difficult as the resolution increases. In other interacting-two-particle cases, we were able to use symmetry to make the problem easier.

[2]

While the chain of successively heavier particles listed in our measurement device is indisputably silly, the point is just to illustrate that we are moving up the size scale from microscopic to macroscopic. It would be very impractical to build a device like this. A better approach is that of the photomultiplier, where all the particles are electrons just with more of them at each stage. This would be more difficult to visualize, though, as a multi-particle wave function.