Double slit¶
The double slit experiment is a classic demonstration of many of the key properties of quantum mechanics. As first performed by Young in 1801, the experiment shows that light has wave-like properties. A light source is incident on a screen with two parallel slits cut in it. When the light passes through the slits, the light diffracts and spreads out from both slits. The light hitting a second screen is then viewed: the overlapping sources of light create interference fringes. As we have seen above, interference fringes are a characteristic of overlapping classical or quantum waves.
A later version of the experiment was carried out with a very dim light source, such that individual particles of light (photons) would hit the screen one at a time. In this case, the screen was a photographic plate, so the photons would create individual spots which over time, build up into the expected interference pattern. This demonstrates that a single particle actually travels through both slits, and interferes with itself. Such interference is not surprising if we already know that what we call “particles” are actually waves, but it would be quite surprising if we pictured particles as little balls. The nature of particles revealed by this experiment is sometimes, confusingly, called “wave-particle duality.” It is perhaps better to consider the photon as being a quantum wave, as described above, with the observed dots on the screen arising from the way in which those waves are measured by the screen. This distinction will be revisited below after we have developed some other key ideas.
Still later, the double slit experiment was also demonstrated using other particles such as electrons, atoms, and molecules, thus proving that massive particles also are described by quantum waves.
The version of the double slit experiment that we will discuss now is the so-called “which path experiment.” In the usual double slit experiment we do not know which slit the particle goes through. Indeed, we would say that the particle goes through both slits. But what if we try to somehow detect which slit the particle goes through? The standard answer to this question is mystifying: If you find out which slit the particle goes through, then the wave function “collapses” and now is only going through the one slit that you measured. As such, there will no longer be an interference pattern on the second screen. Somehow the very act of measurement has caused a sudden and irreversible change to the wave function!
The effect of measurement on a quantum state is included in the standard theory of quantum mechanics as an axiom. Another axiom, for example, is that particles are described by waves as described above. A strange aspect of the measurement axiom is that no one knows how to define what “measurement” actually means. This is problematic, in that it is impossible to falsify this theory without a precise definition of “measurement.” Recent work has questioned whether this measurement axiom is really necessary, or whether it is just a phenomenon that follows from the wave behavior.
In this section, we will see that the “which path” result is not so mystifying after all. (As long as we have accepted the concept of two particle states described above, which is admittedly, a bit mystifying itself. But at least we don’t add mystification on top of mystification.) What we will see is that we don’t need to invoke the measurement axiom at all to understand why the interference goes away in the double slit experiment.
We will first consider a somewhat more straightforward version of the double slit experiment, based on the Mach-Zehnder interferometer. A diagram of the Mach-Zehnder interferometer is shown in Fig. 3.1. A source of particles (typically a laser, though possibly a source of massive particles) is split into two paths by a beam splitter (a mirror that reflects half of a wave packet and transmits half of a wave packet.) The wave packet of a given particle (shown in green) is thus split into two components as was seen, for example, for the Klein-Gordon wave partially tunneling through a narrow barrier (Fig. 1.5). The two components of the particle are reflected off of mirrors to change their direction (similar to how the Klein-Gordon wave reflects off a wide barrier, Fig. 1.4). We place a screen at the point where the two paths come together, and just as in the double slit experiment, we expect to see interference fringes due to interference of the two components of the wave packet.
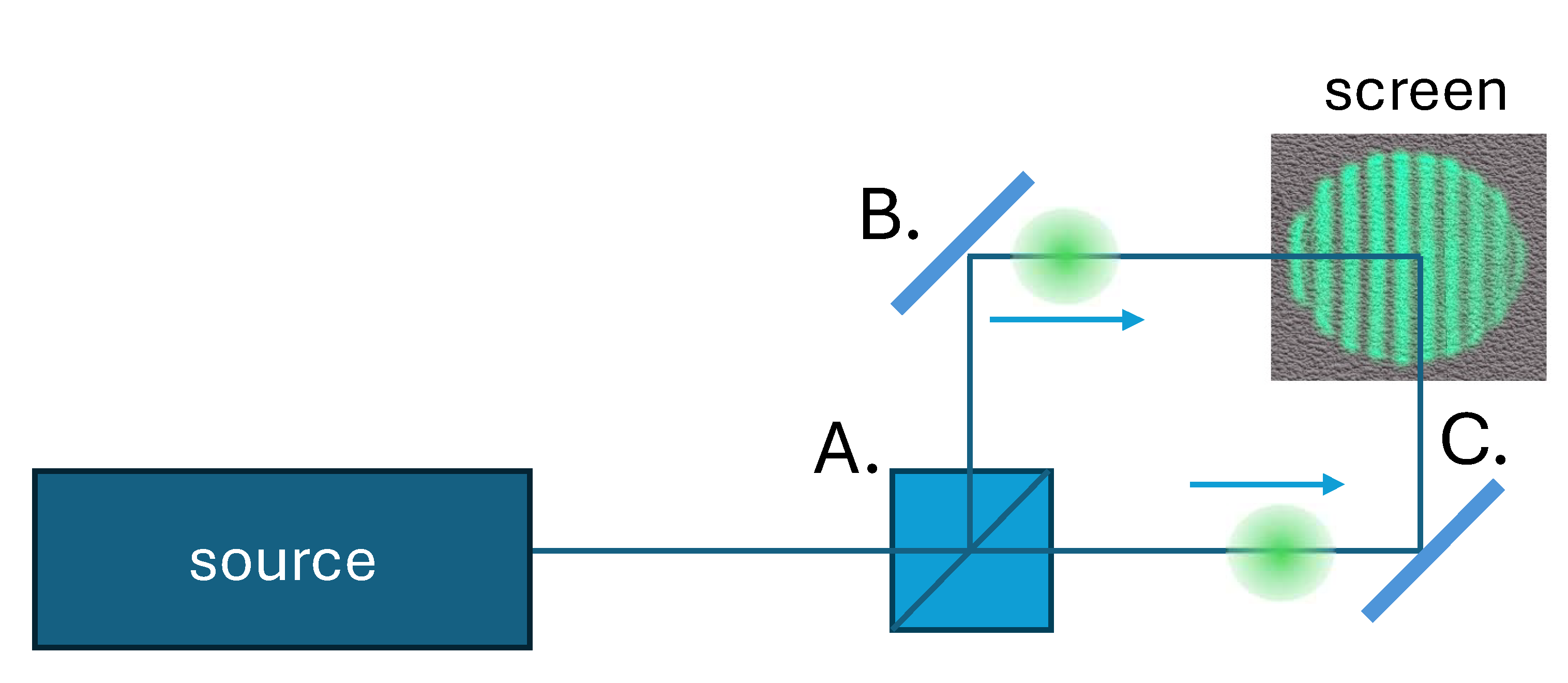
The particle travels down both arms of the Mach-Zehnder interferometer. The “which path” argument would be that if you determine by which arm the particle travels, the interference fringes would disappear. One possible idea for determining the path by which the particle travels would be to measure the recoil of one of the mirrors when the particle bounces off of it. Since the momentum of the particle changes when it reflects off the mirror, the mirror itself must pick up an opposite change in momentum, according to conservation of momentum. Of course, in the standard setup the momentum of the particle is tiny compared to the mass of a normal mirror, so it is sort of absurd to try to think about measuring the recoil. But what if the mirror itself was microscopic? That is the case we will look at.
In fact, we will further simplify the experiment. Instead of drawing the diagram in two dimensions, as in Fig. 3.1, we will reduce the situation to one dimension, as in all the previous examples. As already noted in the previous paragraph, the initial beamsplitter may be replaced by a narrow barrier that splits a wave packet into two components, and mirrors can be replaced by completely reflecting barriers.
The only complication is that if we restrict things to only move along a line, then it’s not possible to get the beamsplitter and mirrors in place at once without the particle hitting the beamsplitter a second time [1]. Instead, we’ll split the process into parts. First, the wave packet will be split into two components traveling away from each other. One component will then reflect off a mirror, resulting in two separated components traveling in the same direction. Finally, the other component will reflect off a mirror, recombining the two components of the wave packet. We could imagine that we somehow yank the beamsplitter out of the setup after the wave packet has been split, but before the particle has returned after reflecting off the mirror. Or more realistically, we could realize that everything should work the same in two dimensions, but for ease of visualization we need to do it in one dimension.
In the examples above, we illustrated splitting and reflection of a wave packet off of an external barrier (Fig. 1.4 and Fig. 1.5). Our goal, however, will be to demonstrate the entire process without resorting to unspecified external barriers. If we want to discuss the recoil of the mirror, we had better specify what the mirror is made of. Specifically, our mirrors and beamsplitters will just be other particles, interacting with our particle of interest, as described by multi-particle wave functions. In all cases, “particle 1” will refer to the particle traveling through the interferometer. And the role of mirrors and beamsplitters will be played by “particle 2.”
First, we demonstrate a beamsplitter (Fig. 3.2). The particle 1 wave packet will interact with a second, much heavier particle 2 that serves as the beamsplitter. The second particle will initially be in a very narrow wave packet [2]. Note that the vertical axis of the video is zoomed in because the beamsplitter wave packet is so narrow. As before, the white dotted line indicates where the two particles meet (now not at 45 degrees because of the zoom-in on the vertical axis). The range of the interaction is very small, so the two particles really only interact where their wave functions overlap. The strength of the interaction is set so that particle 1 is partially transmitted and partially reflected. Because the beamsplitter is so heavy, it barely recoils when it interacts with particle 1. As such, the two particles remain mostly non-entangled after the interaction. A slight vertical offset of the two components can be seen, which indicates a slight entanglement. As seen above, complete entanglement would be indicated by the wave packets being completely offset in both directions. We could reduce the entanglement further just by making the beamsplitter more massive, but it becomes inconvenient to simulate.
Next, we will start from the state after the beamsplitter, and look at the reflection of one of the particle 1 wave packet components off of a “mirror,” which is actually a third particle (Fig. 3.3). This particle will again be very heavy with a narrow wave packet, but this time with an interaction strong enough that one component of the particle 1 wave packet will be completely reflected. We will assume that the entanglement of our particle with the beamsplitter in the previous step was negligible, so we can separate the wave function of particle 1 from that of the beamsplitter. Now we visualize a new two-particle wave function describing our particle 1 and the “mirror” particle. In the movie, we start from a state that looks like the end of the beamsplitter example, with particle 1 in a state with two packets moving apart from each other. One packet collides with the mirror particle at the dashed line, and completely reflects. Again, the vertical axis is zoomed in because the wave packet of the mirror particle is so narrow. Also like the beamsplitter, we see a slight vertical offset between the two parts of the packet after the reflection. This indicates a slight entanglement between that particle and mirror, which would become smaller if the mirror were even more heavy.
At this point, the particle 1 wave packet now has two spatially separated components traveling in the same direction. We are ready for the final mirror (Fig. 3.4). This is now a fourth particle, just like the previous “mirror” particle, but on the other side of particle 1. Just as before, when the leading component of the packet reaches the mirror particle (at the white dotted line) it is completely reflected, sending it back towards the other part of the wave packet.
Now the magic happens when the two components overlap while traveling in opposite directions. Clear fringes appear, due to interference. This should not be surprising, as long as we didn’t forget that these packets are actually made up of some number of waves. (We just haven’t been looking at those waves, because we have been combining the real and imaginary components via the amplitude squared.) But the situation is just as was shown before, such as in Fig. 1.6.
Having shown the normal double slit interference, we now turn to a situation where we can determine which path the particle has taken. As mentioned, the plan will be to observe a recoil in the final mirror when particle 1 reflects off of it. In the version shown so far, the mirror particles are much heavier (200x) than particle 1, so they have only a small recoil. This causes the small vertical shift between the two components seen in the previous examples. However, we can clearly see that this vertical shift is less than the width of the mirror wave packet. That means that the difference between the mirror’s original position and its recoiled position doesn’t conclusively reveal whether particle 1 reflected off of it.
Of course, if we want to get a bigger recoil in the mirror particle, we should just make it lighter. However, at the same time, we don’t want to change the trajectory of particle 1 upon reflection. We can make sure that the particle 1 trajectory stays the same by giving the mirror equal and opposite momentum to particle 1. Actually, we did this without mentioning it in the previous case – when the mirror particle is very heavy it doesn’t make much difference. By giving particle 1 and the mirror equal and opposite initial momentum, we guarantee that particle 1 will just experience a flipping of its momentum when it reflects, as it would if the mirror were infinitely heavy. The initial velocity of the mirror (particle 2) will now be visible in the video as an initial upwards motion of the blobs in addition to the initial leftward motion due to the particle 1 velocity.
In the case where the mass of the final mirror is just twice the mass of particle 1 (Fig. 3.5), we see that the situation is quite different, and no interference occurs. (Note that the particle 2 axis is not zoomed in any more.) Just from watching the video, the reason why there is no interference is obvious – the two blobs in the two-particle wave function never overlap. Recall that this is all happening in one dimension. Near the end of the video when the two blobs pass each other at the same value of \(x_1\), the two components of particle 1 are actually overlapping at the same position. But because those components are now entangled with two non-overlapping components of particle 2, the two blobs to not overlap.
Though it’s clear that no overlap means no interference, the reason why they don’t overlap is a little confusing. But it is important, so let’s take some time to think about it. The reason why the two components do not overlap is because the collision of one component of particle 1 with the mirror particle has caused one component of the mirror particle to split off and become entangled with that component of particle 1. This is the first yellow blob that collides and heads off in a new direction. The remaining component of the mirror particle is now entangled with the component of particle 1 that did not collide. These components are shown as the yellow blob that keeps moving in the same direction. We can see the entanglement immediately by the fact that the two blobs are now not aligned either horizontally or vertically. You may recall that exactly the same effect was shown back in Fig. 2.6 in the original demonstration of the entanglement of two particles. The system is now in a state where two things are true: particle 1 has collided with the mirror and caused it to significantly recoil and particle 1 has not yet collided with the mirror which remains in its original state of motion.
We can see that the key factor for removing the interference is that the two components have separated sufficiently far in the vertical direction such that they do not overlap when they cross in the horizontal direction. Again, both particles are, in fact, only moving along a line in one dimension. When the two components move past each other in the horizontal direction (whether overlapping or not in the vertical direction), those two components are actually overlapping in space along the line. But if the particles are entangled in such a way that the components do not overlap in the vertical direction, the two components pass right through each other, as if the other weren’t there. Or in other words, they do not interfere with each other.
At the risk of being repetitive, the key factor for removing the interference is that the two blobs have separated sufficiently far in the vertical direction such that they do not overlap when they cross in the horizontal direction. So the recoil of the mirror must be larger than the width of the mirror wave packet [3]. This means that in the case of no interference, the recoil of the mirror is sufficient to clearly distinguish whether the collision has taken place or not. In other words, the recoil of the mirror is sufficient to reveal which path the particle took.
To summarize: when the mirror recoils enough that we can conclusively distinguish between recoil and no recoil, the interference goes away. If the recoil of the mirror does not give us sufficient information to determine whether a collision took place or not, then the interference remains.
The above example has shown that the “which path” effect can be understood by looking only at the evolution of particles moving according to the quantum wave equation (the Schrödinger equation). We did not need to invoke any additional axioms about measurement. In this case, at least, the measurement axiom appears to be redundant.
The fact that the quantum wave behavior seen above replicates the prediction of the measurement axiom raises the question as to whether what has happened here constitutes a “measurement.” The process has at least one characteristic of a measurement: information about the state of particle 1 was transferred to another system. If particle 1 had been in a wave packet traveling exclusively along one arm or the other, the resulting recoil of the sufficiently light mirror 2 particle would conclusively reveal which arm it was in.
On the other hand, there are several aspects of this example that might give us pause before we declare that a measurement has occurred. First and foremost, the resulting state does not just give a single measurement outcome. Instead, when particle 1 was simultaneously traveling in both paths, the mirror particle both recoils and does not recoil. We can only say that the recoil is correlated with one path, and the lack of recoil is correlated with the other path. A second objection is that, while information about the path has been transferred, the vessel for that information (mirror 2) is still microscopic. If the result of a measurement is something that we should, at least in principle, be able to perceive through our senses, then there must be more to the process of measurement.
The second objection – that the object doing the measurement is still microscopic – is probably easier to deal with than the first. Perhaps the recoil of the microscopic mirror is just the first step of a measurement process. Once the information is transferred on the micro-scale, we then need some form of amplification to transfer that information to larger and larger systems. For example, we might want that information to eventually be displayed by moving a pointer on a dial that we can look at with our eyes. We will discuss this amplification process more later. It is not without complications: as the information is amplified greater numbers of particles must be involved, which will generally have a greater chance of accidentally interacting with other particles in undesired ways.
The first objection – that we didn’t obtain just a single measurement outcome – might be trickier. But a simple resolution to that issue would be that our insistence on a single measurement outcome is misplaced. Maybe even at the macroscopic scale, both measurement outcomes occur. This is known as the Everett interpretation, or the Many Worlds interpretation, of quantum mechanics. This, too, will be discussed further below.
Since the microscopic interaction and subsequent entanglement of the particle and mirror seen above bears some resemblance to a measurement, we will refer to it as a “micromeasurement.” This micromeasurement transferred information about the position of the particle to the mirror. In the next section, we will develop another micromeasurement to measure a different quantity: the phase difference between two components of a wave packet.
Footnotes