Quantized waves¶
In order to develop some ideas needed for the next section, here we’ll take a further look into some wave properties when waves are confined to a finite region. Despite the title of this section, the sort of quantization described here applies to both classical waves and quantum waves.
Though we didn’t mention it at the time, the original example of a jump rope stretched between two people was an example of a wave confined to a finite region. Naturally, the wave cannot propagate past the ends of the jump rope. If both people hold their ends at a fixed position, then there is a constraint on what sorts of waves can exist on the jump rope. Specifically, the only waves that can exist on the jump rope are ones that have zero displacement at either end.
Figure 4.1 shows examples of sinusoidal waves that can exist on a jump rope fixed at both ends, and one that cannot. We see that only certain wavelengths are permitted. Consequently, because the wavelength is related to the frequency, only some frequencies are permitted. One might say that the frequencies are quantized.
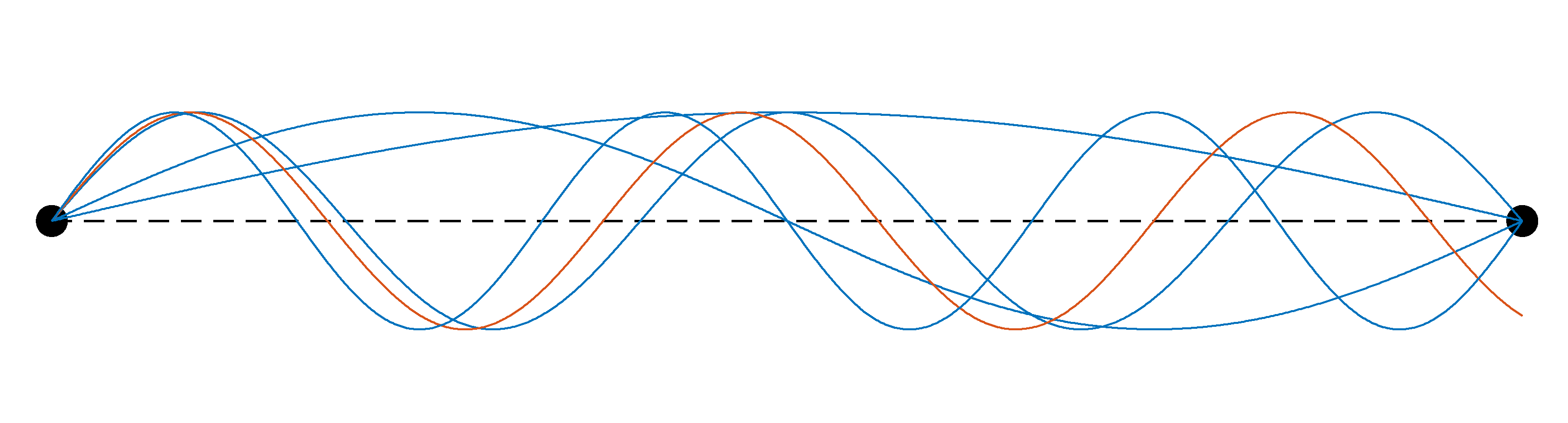
Of course, waves don’t have to be just simple sinusoids as shown in Fig. 4.1. For example, a wave on the jump rope could be the superposition of two, or more, different permitted sinusoidal waves. Such a wave would also satisfy the boundary condition of zero displacement at the ends. In fact, it turns out that any wave that satisfies the boundary conditions can be described as a superposition of the permitted sinusoids. (This might be surprising if you aren’t familiar with the idea of Fourier series, but it’s a mathematical fact!) For example, the pulse-like wave packets that we looked at in the section Classical waves could be expressed as a superposition of the allowed sinusoids (at least after Alice has finished launching the pulse by jerking her end up and down). We would say that the allowed sinusoids are a complete basis, recalling that basis functions are waves that we superpose together to describe other waves.
It can be useful to think of a wave on a string as a superposition of the allowed sinusoids. This is because these basis functions evolve in time in a simple way — they each just oscillate at a particular frequency. If, at some point in time, we know how to describe the displacement of a wave as a superposition of these basis functions, then we can easily find the displacement at any other time. We just have to take the wave apart into its sinusoidal components, oscillate each sinusoidal component in time according to its frequency, and then add them all back together.
So far in this section we have been talking about the simple case of a uniform string fixed at both ends, but things get more interesting if we allow the properties of the string to change along its length, and more so if we consider the case of Klein-Gordon waves. Recall that Klein-Gordon waves occur in classical situations, such as the tennis net model where we consider waves on a cable stretched between two posts with an elastic net connecting the cable to the ground. And the same type of Klein-Gordon waves also describe the quantum behavior of particles.
We previously saw what happens to a Klein-Gordon wave when the net becomes stiffer over either one half of the length, or over a short “barrier” region. The former case created a barrier that reflected an incoming wave. Because Klein-Gordon waves have a minimum frequency (due to the stiffness of the net, or the rest mass of a particle), a barrier can be completely reflecting — waves with a sufficiently low frequency cannot propagate into the barrier region. The latter case demonstrated the fact that the waves can “tunnel” through a barrier. Though these low frequency waves cannot propagate in the barrier, they do penetrate a small distance and can then continue propagating on the other side.
Now we will see what happens to a Klein-Gordon wave when the stiffness of the net is increased everywhere except over a small region. This is not really anything new. The steps from the less-stiff region to the more-stiff exterior again form barriers that sufficiently low frequencies cannot overcome. But now these steps serve to confine the wave within a region. So now we have a wave confined not because we are holding the ends of string fixed, but because we are creating a finite region — a so-called well – where the wave is only allowed to propagate.
The confined Klein-Gordon waves are similar to the string with fixed ends, with a few differences. First, instead of requiring the displacement to be strictly zero at the boundaries, the Klein-Gordon wave can penetrate a bit into the barriers. Nonetheless, this still defines a similar boundary condition that only allows certain wavelengths or frequencies within the well. A second difference is that the waves are only confined for waves of sufficiently low frequency such that they cannot propagate beyond the barriers. So while a string fixed at both ends can have an infinite number of allowed waves, with arbitrarily short wavelength, there will only be a finite number of Klein-Gordon waves confined by a well.
Let’s look at some examples of Klein-Gordon waves confined to a well. Figure 4.2 shows the lowest frequency (longest wavelength) Klein-Gordon wave in the well illustrated in gray. The top panel shows the wave displacement \(d\). As in previous examples such as Fig. 1.3, we are in the situation where the minimum frequency from the tennis net is much larger than the frequency from any waves on the string. As such, the displacement shows extremely rapid oscillations that are hard to look at and don’t tell us much. As before, we can remove these fast oscillations be decomposing the wave as
\[d(x,t) = u(x,t) \cos{(mt)} + v(x,t) \sin{(mt)}.\]
The much slower waves \(u\) and \(v\) are shown in the middle panel. They look a little bit like half of a wavelength of a sinusoid (a single peak or trough), but with little tails that penetrate into the barriers a bit. We can see that they oscillate slowly, and out of phase with each other such that one of them is a maximum or minimum when the other is zero. The frequency of oscillation that we see in \(u\) and \(v\) is the extra frequency due to the wave, above that from the net alone.
Finally, at the bottom of Fig. 4.2, we plot the combined amplitude squared \(u^2+v^2\). Because, as just mentioned, \(u\) is a maximum or minimum when \(v\) is zero, and vice versa, the amplitude squared remains constant in time.
The Klein-Gordon wave above has been discussed in terms of a classical wave on an (idealized) tennis net. But as we have already learned, the same type of wave describes the quantum behavior of a particle. In this light, we can re-interpret the minimum frequency as the rest mass of the particle (which we wish to ignore) and the functions \(u\) and \(v\) as the real and imaginary parts of a complex wave function \(\Psi\). The amplitude squared in the bottom plot is then \(|\Psi|^2\). None of the phenomena in this section are different depending on whether we think of these waves as representing something classical or quantum. (The difference comes in the interpretation of what the wave represents, and also when we consider more than one particle and entanglement enters the picture.)
As a next example, Fig. 4.3 shows the next lowest frequency confined Klein-Gordon wave in the same potential, with the three panels again showing the wave displacement, the slow components with the minimum frequency stripped off, and the amplitude squared. Now we can see that shape of the wave is something like a single period of a sinusoid, with both a peak and a trough. Now the tails penetrate a little farther into the barrier because the higher frequency of the this wave is closer to being able to overcome the barriers. Other than that, the behavior is similar to Fig. 4.2, with the two components oscillating out of phase, such that their amplitude squared is constant.
You can probably imagine what the next-lowest-frequency confined wave would look like: something like one and a half wavelengths (peak-trough-peak or vice versa). That guess would be correct, except for the fact that in the well shown here, the third-highest frequency confined wave would actually have high enough frequency to escape over the barriers and propagate away. So there are only two distinct confined waves in this case (the ones shown). Any higher frequency waves can propagate away like the wave packets we have been looking at previously.
The two confined waves shown in Fig. 4.2 and Fig. 4.3, however, are not the only waves that can exist in the well: we can also have superpositions of the two. We can add them together in any proportion that we like. Figure 4.4 shows what happens when we add them together in equal proportions.
With a superposition of the two sinusoid-like confined waves, we now have a more intricate behavior of the two components shown in the middle panel. Though it is a bit difficult to follow, we can think of this as interference between the two different waves. The most striking result of this is seen in the bottom panel showing the amplitude squared. Unlike the previous two cases, where the amplitude squared was constant, here it oscillates from one side of the well to the other. This occurs because of how the interference changes as the waves evolve with their different frequencies. We started the wave with the two component waves added together. But because they have different frequency, over time they evolve to become a wave with the two components subtracted. This shifts the interference to the opposite side. Waiting still longer, they will come back to the original state with the waves added.
If we interpret this Klein-Gordon wave as a quantum particle, then the waves in the well are called a two-level system, because any wave is composed from two possible basis waves. A quantum two-level system is also known as a qubit, short for “quantum bit” in analogy to a “bit” – a classical two-state system. Such systems are the building blocks for quantum computers and other emerging quantum technologies.
In the next section, we will see how we can use these confined waves in combination with propagating wave packets to delve more deeply into the nature of measurements in quantum mechanics.