Born’s Rule¶
Thus far, we have been rather vague about what the amplitude of the wave function actually represents. We have said that non-zero amplitude at some position means that a particle is “located” at that position (and thus a particle may be located at many positions simultaneously). And we have said that zero amplitude means that a particle is not located at that position. But this is a binary distinction, whereas the amplitude is a continuously adjustable variable. What is different about a larger vs. smaller amplitude? If we let the amplitude at some position become arbitrarily small, is the particle still located there?
We have relegated these important questions to the end because their answers require many of the ideas we have developed: entanglement, amplification, complementary observables, branching, and perhaps most puzzling, our perception of branching.
If you have taken any course in quantum mechanics, you probably know the standard answer to the questions above. According to the measurement axiom, the amplitude squared of the wave function at some position is supposed to tell you the probability that you will measure a particle at that position. That is, when you measure the position of a particle, the wave function “collapses” to a narrower one that corresponds to one particular position. Which position? It gets picked at random, with probability given by the amplitude squared of the wave function.
The standard probabilistic measurement axiom seems simple, but it is really rather strange. This prompted Einstein’s famous quote, paraphrased as “God does not play dice.” Consider the following. In every other context, probabilities have to do with ignorance. We can make a game of betting on rolls of the dice because we don’t know how the dice will land. Presumably, a sufficiently powerful computer could take a video of dice flying through the air, and predict how they will land. It might be necessary to take into account air currents in the room, imperfections in the tabletop, etc., but it should be possible for a sufficiently powerful computer, or a sufficiently omniscient god. But we humans cannot make such a prediction with certainty — we are ignorant. The best we can do is quantify our ignorance in the form of probabilities.
But the normal understanding of probability — the quantifying of ignorance — does not quite work in the case of the quantum measurement axiom. A wave function in a superposition of two separated wave packets does not mean that the particle is either at one position or the other, but we just don’t know which. If that were the case, how could we understand measurements of complementary observables? We have seen that the wave function not only specifies the outcome of a position measurement, but also complementary measurements such as the phase difference between two packets. The standard measurement axiom says the outcomes of complementary measurements are also probabilistic: we can rewrite a superposition of two separated wave packets as a superposition of in-phase and out-of-phase pairs of packets. The amplitude corresponding to the in-phase pair, squared, should be the probability of measuring in-phase (and that the wave function collapses to become equal in-phase packets only), and vice versa. The normal understanding of probability fails here: was the particle in one of two positions, or in one of two phase differences? It can appear either way, depending on which one we measure.
So it seems that the sort of probability of collapse invoked in the measurement axiom is an entirely new sort of probability. There is no mechanism behind it. As far as we know, if true, it would be the only completely random process. Perhaps even god couldn’t predict it.
So of course, we are going to try to explain the observed behavior of measurements without using the quantum measurement axiom.
Unequal amplitudes¶
First let’s look at a few examples of wave functions with unequal superpositions. We will see how the micromeasurements still capture the behavior of the measurement axiom, with two exceptions: the absence of collapse, and (so far) the absence of any idea of probabilities.
Figure 10.1 shows a single particle wave function initially in a superposition of two packets with different amplitude. We see that the picture is largely similar to the case when the packets are equal, except the interference fringes don’t make it all the way down to zero. Here, we have set one packet to have double the amplitude of the other. Therefore, one packet has four times larger amplitude squared. If we let \(\Psi_a\) and \(\Psi_b\) represent the packets initially on the left and right, but with equal amplitude, then we can write the initial state shown here as
Now let’s look at the situation when an unequal pair of wave packets interacts with a second particle. The scenario in Fig. 10.2 is just like the “which path” position micromeasurement in the double slit section (see Fig. 3.5) but now instead of a 50/50 beam splitter, one path has double the amplitude of the other. The result is not too surprising. The two blobs just collide as before, with the two blobs keeping the same ratio of amplitudes. The final state is again entangled, but with one blob having double the amplitude (4 times the amplitude squared) of the other.
Finally, Fig. 10.3 shows a phase micromeasurement on the particle with two unequal packets. The initial state is \(\Psi = \Psi_a + 2 \Psi_b\) as also shown in Fig. 10.1. \(\Psi_a\) and \(\Psi_b\) are in phase with each other. As usual, we place the atom phase sensor at the midpoint between the two packets. Perhaps we are not surprised that we see a partial rotation from the \(|+\rangle\) to \(|-\rangle\) states of the atom, since we saw above that we only get partial interference in this case. But look carefully at the final state in Fig 10.3; the amplitudes are not in a 2:1 ratio — the blue one is smaller than half the red one.
We can understand what is going on in the complementary measurement shown in Fig 10.3 if we write the wave function in terms of states with definite phase, instead of definite position. So a little bit of math: As we had defined back in the Complementary observables section, the states with well-defined phase difference are \(\Psi_0 = \Psi_b + \Psi_a\) and \(\Psi_\pi = \Psi_b - \Psi_a\). We can add the two together to find \(\Psi_0 + \Psi_\pi = 2\Psi_b\) or subtract them to find \(\Psi_0 - \Psi_\pi = 2\Psi_a\). We can then use these equations to write our initial state
Thus we can alternatively view our initial state as one with 3 times the amplitude for in-phase as compared to the amplitude for out-of-phase. The final state reflects this split, with 3 times the amplitude correlated with \(|-\rangle\) (the in-phase micromeasurement result), as compared to the the amplitude correlated with \(|+\rangle\) (the out-of-phase result).
Moreover, looking at the final state of Fig 10.3, we see that each state of the atom is now correlated with an equal superposition of two packets, which are out-of-phase when correlated with \(|+\rangle\) and in-phase when correlated with \(|-\rangle\). That is, each state of the atom is correlated with a wave function with well-defined phase difference. Those two components of the wave function just correspond to the two terms in the initial state \(\frac{3}{2} \Psi_0 + \frac{1}{2} \Psi_\pi\). The first term becomes correlated with \(|-\rangle\) and the second with \(|+\rangle\).
The above figures illustrate that our complementary micromeasurements still “work” with uneven initial wave packets. As compared to the standard measurement axiom, everything comes out the same, with the following exceptions. According to the standard axiom, one of the two entangled components should disappear upon measurement, and the one that remains should do so with a probability proportional to its amplitude squared. That is, in Fig. 10.2, after the measurement one of the blobs should disappear completely. The brighter one should disappear with probability 1/5, or the dimmer one with probability 4/5. (Given their amplitudes squared, one should be 4x more likely than the other, and the probabilities must add to 1.) Or in Fig. 10.3, either the wave function correlated with \(|+\rangle\) should disappear (with probability 9/10) or the wave function correlated with \(|-\rangle\) should disappear (with probability 1/10). Again, this is because the amplitudes squared are in a ratio of 9:1.
Of the differences between the micromeasurement and the standard measurement axiom, we know that we don’t need to worry about “collapse” part if we are thinking in the Many Worlds picture. We just accept that multiple outcomes do occur. The probabilities, however, are key to our observations of quantum phenomena. Even if the wave function says that multiple measurement outcomes occur, we perceive that one of them has occurred with a particular probability.
Branch ignorance¶
In the previous section, we discussed why we only perceive a singular measurement outcome. The idea is that once a macroscopic system has become thoroughly entangled with the system being measured, any subsequent effect used to confirm the measurement outcome must be correlated with the outcome in that particular component of the wave function. The “macroscopic system” could be a computer programmed to follow up on a measurement with additional checks or it could be you using your senses and brain to remember, think about, and double check the outcome.
If the measured system was initially in a two-part superposition of the measured observable, we can picture the wave function as two blobs, initially only separated along the dimension(s) corresponding to that system. Once the measurement device becomes entangled with the system, the blobs become misaligned in many, many dimensions. Ultimately after a successful measurement, we still have two blobs, but one containing a representation of the measurement device with one outcome, and the other the other outcome.
This leads us to the key idea: before you become entangled with the system-to-be-measured, you are ignorant of which outcome you will perceive. If you are familiar with the behavior of the Schrödinger equation (and you are, having studied this whole tutorial so far), then you are aware that both outcomes will occur, but that you will feel like you are perceiving only one of them. According to the Many Worlds picture, you actually perceive both outcomes. We might say that there is a world where you perceive one outcome, and another world where you perceive the other one. It’s like there are two versions of you. Before the measurement, we could say that there is just one version of you, or perhaps two identical versions. After the measurement, the two versions perceive different outcomes. Of course, you still feel like the singular you. Even if you believe there is another version of you, the other you feels like an impostor. Though surely the other version feels the same way about you!
The ignorance about which outcome you will perceive can be quantified with a probability. The concrete use of probabilities is that they allow us to make predictions in the face of ignorance. So in the interest of being concrete, let’s think about this in the context of trying to make good predictions.
Quantum gambling¶
Let’s say you are a researcher working in a laboratory. You have constructed an experiment that takes a single particle, puts it through a beam splitter (maybe 50/50, maybe not), then performs the “which path” measurement. This is just the experiment we have described at length here, most recently in Fig. 10.2 followed up by the “marble run” amplification. Recall that the two possible outcomes of the marble run experiment are the pointer pointing to “left” and “right.”
Things can be a little slow in the lab sometimes, so you decide to spice it up a little. You say to your colleague Dr. Vincent, “What do you say we make this experiment interesting? Let’s put some money on the outcome!”
“Okay,” says your colleague, who goes by the name Vinnie the Shark. “I’ll give you odds on the outcome, and you can decide whether you want to take the bet.”
In case you’re not into sports betting, here’s how it works. The person offering the bet (Vinnie the Shark) gives odds, like 4-1 odds of “left.” This means that Vinnie thinks that “right” is 4 times more likely than “left.” If you think Vinnie’s estimation of the odds is wrong, you might wish to take the bet. If you believe the odds of “left” are better than Vinnie thought, you can place a bet, say $20, on “left.” If “left” is indeed the outcome, then Vinnie has to give you $80 (4x your bet). But if the outcome is “right,” then you have to give Vinnie the $20 (1x your bet). (And if you don’t, he might just break all the glassware on your lab bench.) On the other hand, if you think Vinnie is wrong the other way and has underestimated the chances of “right,” you can bet $20 on “right.” Then if the outcome is indeed “right”, Vinnie gives you just $5 (4x less than your bet, since after all, Vinnie did say that “right” was favored.) And again, if you bet wrong and the outcome is “left” you have to give Vinnie the $20.
The upshot of these betting rules is that whoever can better estimate the odds will come out ahead in the long run, after many bets are made. But there is a twist in the Many Worlds scenario: both outcomes occur! That means that no matter what bet you make, there will be a happy version of you that wins, and a sad version of you that loses. Does that mean that there is no way to win? Only in the same way that you can’t guarantee a win on any one bet. Instead you hope that in the long run, if you bet sufficiently intelligently, you will come out ahead in the end. Of course, you might not — you might just be extremely unlucky and lose every time despite making good bets. Likewise, you hope that the different versions of you, on the balance, come out ahead. There will be some unlucky version that loses every time, but we hope that the happiness of the happy versions outweighs the sadness of the sad versions. All right. Now let’s try to be more precise.
Even odds¶
To start, say we place a 50/50 beam splitter in our experiment, just as in Fig. 3.2. This puts the particle into an equal superposition of two locations. Vinnie thinks for a minute and says, “I’ll give you 4:1 odds on ‘left’.”
Now although Vinnie’s biceps may be threatening to burst through the sleeves of his lab coat, he is not the sharpest when it comes to the Schrödinger equation. Your initial thought is that these odds don’t make sense. If the two wave packets in the superposition have the same amplitude, why is Vinnie thinking that it is 4 times more likely to measure the packet on the right than on the left? It seems more likely that the odds should be an even 1:1.
While you are pondering this, you notice Vinnie surreptitiously doing something. While he thinks you are not looking, he is slipping some extra mirrors into the experiment, so as to swap the two packets of a particle on each side of the marble run apparatus! This will have the effect of flipping the outcome of the experiment. The snake! But actually, his attempt to cheat you gives you an idea — now you are firmly convinced that the odds are 1:1 and that his trickery didn’t make any difference. How did you know?
Your reasoning is as follows. When the measurement is taking place, we know that lots of additional particles are becoming entangled with the particle being measured. Let’s consider one such particle to be a photon from the ceiling lights in the lab. With the apparatus particle in an equal superposition of two well-separated positions, the photon can become entangled with it. This is like the situation shown in Fig. 8.7. In one component of the state, the photon will bounce off the leading packet of the particle, and in the other component, the photon will bounce off the trailing packet (still in its divot). Next let’s say that both components of the photon fly out of the lab window, and before you know it, they are two towns over.
Just considering the photon and apparatus particle, the state now looks something like the top left panel of Fig. 10.4. Note that the components of both particles are separated by a few centimeters, but the photon packets are now kilometers away from the apparatus. But no matter, it’s just the entangled state we have looked at many times already. Now let’s look at the effect of Vinnie’s dastardly swap (top right of Fig. 10.4). Say Vinnie’s swap occurs after the photon and particle have interacted but before the measurement has completed with the motion of the pointer. So that means we take the state at the top left of Fig. 10.4 and swap the apparatus particle components. Or in other words, we swap the two blobs in the horizontal direction.
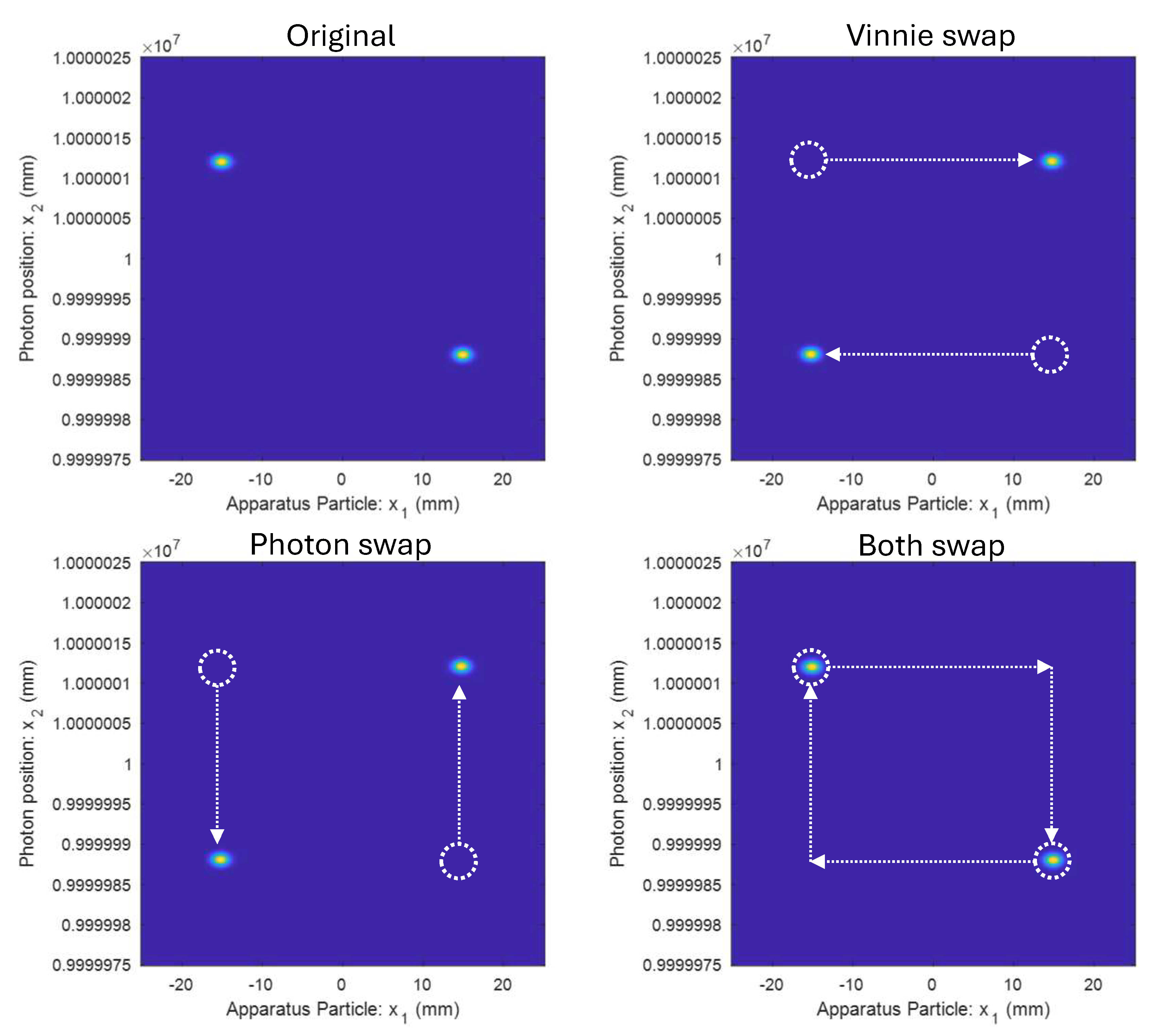
Comparing the top left (before swap) and top right (after swap) in Fig. 10.4, should we assign different probabilities to the measurement outcome for these two states? Maybe — they are after all, different states. But here’s the catch. Two towns over, we have no idea what is happening to that photon. It is possible that the photon has, by chance, encountered some mirrors in a local fun house or department store fitting room, and wound up with its two packets swapped. We would have no way of knowing. In fact, if the photon traveled far enough at the speed of light, it might not be possible for us to find out what happened to it before the measurement has completed.
The bottom row of Fig. 10.4 shows what the state looks like if the distant photon’s packets were swapped, both in the original case (left), and where Vinnie has also swapped our local particle (right).
The crux of the argument is that whatever might be happening to the photon two towns over should not affect the outcome of the measurement in the lab. As we saw in the section on Bell state measurement, such distant changes can affect correlations between distant measurement outcomes, but not individual local measurements in isolation. This means that the two states shown in the bottom row of Fig. 10.4 should have the same probabilities for the perceived measurement outcome in the lab. But the two states in the bottom row are exactly the same as the two states in the top row, just in reversed order. Notably, the two swaps leave us exactly back in the original state! This tells us that Vinnie’s trick cannot have affected the outcome, because for all we know, the distant photon has also swapped its packets and the state is completely unchanged despite Vinnie’s attempts at trickery. Therefore, the conclusion is that the probability of perceiving both outcomes must be equal, since swapping them or leaving them the same can’t change anything.
An astute reader might note that just because the plots in Fig. 10.4 are identical, doesn’t necessarily mean the states are identical, because we do not see the phase when plotting amplitude squared. But we can make the same argument for the phase of the blobs. If, for some reason, Vinnie thinks that the phase is going to affect the measurement probabilities, he could try to trick us by shifting the phase difference between the two packets of the particle in the lab. This likewise shifts the phase difference between the two blobs. But if some interaction, two towns over, happens to shift the phase difference between the two packets of the photon by the opposite amount, then the phase difference between the blobs would be back to the original. By the same argument as above, the phase cannot alter the probabilities of measurement outcomes perceived locally.
So this rather long-winded explanation leads us to the conclusion that the superposition with two equal wave packets will result in you perceiving a measurement of one position with 50% probability, and you perceiving a measurement of the other position with 50% probability. You decide to take Vinnie’s bet, and place $20 on “left” since for some reason Vinnie thought left was 4x less likely than right, and you have determined that it’s actually 50/50. The measurement then finishes running, and you observe the result. There are now two versions of you. One is happy; your bet has paid off. The other is sad; you lost the bet. But because Vinnie gauged the odds incorrectly but you figured it out correctly by using the rules of quantum mechanics, the happy you gets an $80 payout, and sad you only has to pay $20. On the whole, not too bad!
Of course, a single bet is never a sure thing. We can imagine repeating this bet over and over again. An advantageous thing about the Many Worlds picture is that once the worlds have “branched” we can separately focus on just one at a time. So after the outcome of the first measurement, we now have two worlds. In each of those, say Vinnie offers the same bet again, and you again make the same bet of $20 on “left.” After the second measurement, now there will be four worlds. One where you lost both times and paid out $40, two where you won one and lost one for a net profit of $60, and one world where you won twice for a net profit of $160. The upside is certainly outweighing the downside.
If we keep making the same bet many times, then there will be a proliferation of worlds where, looking back on your records, you see that about half the time you have won (and got $80), and half the time you have lost (and paid $20). In these worlds you wind up ahead by about $60 times the number of times you bet. Those versions of you, which are by far the most common versions, are thinking “Ah good, this is coming out just about as I expected from the probabilities.” Of course, there is still one world where you lose every time, and one world where you win every time. But these are just two out of a great number of worlds, and would correspond to the possible but very rare outcome of a really long winning or losing streak. That one version of you is ecstatic (“I can’t believe my luck!!”). The other version is getting their glassware (or worse) broken by Vinnie.
Uneven odds¶
So far, we have argued that the case of equal superposition of the measured observable should lead to a 50/50 outcome of what you end up perceiving. This is essentially based on the idea that there is no way to distinguish between the two cases, so they must be equal. This is similar to the classical argument that a coin flip should have 50/50 odds. There is nothing significant about the two sides of the coin that would lead to a preference for landing on one or the other, so they must be equal. Likewise, there is nothing to set a preference for landing on one of the six faces of a die, so we would conclude that the odds of rolling any particular number on a die will be 1/6.
But what if we measure a quantum state with an unequal superposition? We can take a clue from classical probability. If we want to know the probability of rolling a particular total, say 3, on a pair of dice, it’s a little more complicated than a single die because now the 11 outcomes don’t all have the same probability. The trick is to divide those outcomes up more finely into outcomes that do all have the same probability. Namely, instead of just looking at the totals, we can look at the numbers on each die. There are \(6 \times 6 = 36\) possible rolls. Again, since there is nothing to set a preference for any face on an individual die, all 36 rolls should have equal probability 1/36. Then to get the probability for a certain total, we just have to count how many of the 36 rolls give the desired total. In the case of a total of 3, there are two rolls (1,2) and (2,1) that add to 3. So the probability of rolling a 3 is 1/18.
In the case of probability of perceived quantum measurement outcome, we will make use of the correlations with a distant particle to perform the split into a set of outcomes with equal probability.
Returning to the laboratory and our betting game, let’s now say that we have replaced the beam splitter so that the particle to be measured is split into two packets, one that has greater amplitude than the other. This is like the situation shown in Fig. 10.2. Let’s say that one packet has \(\sqrt{2}\) times the amplitude of the other (and therefore double the amplitude squared). After Vinnie’s (likely) losses in the previous round, he has wised up at least a little. Now he thinks, “The left packet has \(\sqrt{2}\) times the amplitude, so maybe it has \(\sqrt{2}\) times the probability.” So he gives you \(\sqrt{2}\):1 odds on “right.”
You decide to try using the same reasoning as before. We again consider a photon becoming entangled with the the two outcomes of the measurement, resulting in the two blobs shown at the initial state of Fig. 10.5. But now the two blobs have different amplitude. The video then shows what happens if we swap the two packets of the particle in the lab, or the two packets of the photon two towns over, as in Fig. 10.4. But now the two final states are not the same, so we can’t conclude that the two outcomes will be perceived with equal probability. We’ll need to think about a more complicated swapping procedure.
Before getting to the swapping, again consider whether the phase difference between the blobs could make a difference. If Vinnie tries to trick you by shifting the phase difference between the larger and smaller amplitude packets in the lab, could that change the result? Again, we can say that if the distant entangled photon underwent an opposite phase shift two towns over, that would return the state to where it started. The phase shifts affect the blobs in the same way regardless of which particle you are acting on. In this way, we argue that the phase difference cannot affect the outcome, even when the amplitudes are different.
In order to figure out the probabilities by swapping, we need to look at blobs with equal amplitude. That means we are going to have to split up the blobs into some larger number of blobs, all of equal amplitude. We already know a way to split up a blob. We can use a beam splitter on either particle to split a blob in any desired ratio. But how should we divide the blobs to yield blobs of equal amplitude?
To get an idea of how we can divide up wave packets using beam splitters, Fig. 10.6 shows a single-particle wave packet in blue being split into two equal packets by a narrow barrier (the dashed lines). For reference, we also show the same initial wave packet with no barrier in red. At the end of video, we can indeed see two equal packets in both the wave amplitude (top panel) and amplitude squared (bottom panel). Comparing the split blue wave function to the unsplit red wave function, we can see that the amplitude of the split packets is more than half the amplitude of the red packet. As for the amplitude squared, the split packets look quite close to half the amplitude squared of the red packet.
Fig. 10.6 is an example of a general property of the Schrödinger equation: the sum of the amplitudes squared (technically speaking, the integral) remains constant as a wave function evolves in time. The technical term for this is that the evolution is unitary. Note that the sum of the amplitudes squared being constant means that the sum of the amplitudes is generally not constant. This is what we see in Fig. 10.6. The amplitude squared of one packet is split into two equal parts whose amplitudes squared add up to the original. Not so for the amplitude itself.
Now we can answer the question of how to divide up the blobs in our example to make them all equal in amplitude. Recall that one blob has amplitude \(\sqrt{2}\) times greater than the other, and 2 times greater amplitude squared. So if we simply divide the larger amplitude blob into two equal parts, then those two parts will have half the amplitude squared of the original, and all three blobs will have the same amplitude (and the same amplitude squared). We have picked this particular example for its simplicity. As a different example, if one blob had twice the amplitude of the other, then its amplitude squared would be 4 times bigger, and we would need to split it into 4 equal blobs to make them all equal. That is no problem, just more complicated to think about. In general, we might need to split both blobs up into any number of parts. Note that we don’t need to be able to actually do this in reality, we just have to think about it to make an argument about the probabilities.
Our goal will be to show that we can manipulate the state either entirely locally or entirely remotely to obtain identical states, and then compare the two to determine the probabilities.
So once again, Vinnie has tried to trick you by swapping the two packets of a particle in the lab, so as to reverse the measurement outcomes. This is shown at the right of Fig. 10.5. As we saw in the left of that figure, a swap of the photon packets two towns over does not result in the same state. So if you hadn’t noticed Vinnie swapping the particles, his trick might have worked this time. But you did see him, and can think a little bit more about the situation.
What if you, in the lab, make a further modification to the experiment. Starting after Vinnie has swapped the packets (the end of Fig. 10.5, right), you insert some extra mirrors and a beam splitter to send the higher-amplitude packet on the right back to the left, and then be equally split in two right in the middle. This process is shown at the right of Fig. 10.7. By the end, we see that the three packets now all have the same amplitude.
But now, let’s think what would have happened to the state if Vinnie did not make a swap, but instead things only happen to the photon, two towns over. First, the photon’s packets are swapped as shown at the left of Fig. 10.5. Then the high amplitude packet, corresponding to the blob at the lower left, is reflected back sending the blob back upwards. The packet is then split by a beam splitter into two equal parts. This is shown at the left of Fig. 10.7, and is just the same as what we did in the lab, just flipped sideways to act on the photon instead of the particle in the lab.
At the end of Fig. 10.7 we see that the two states are the same, even though one was manipulated by you in the lab, and the other came about from distant events that you have no way of knowing if they occurred or not.
Let’s consider one final swap, two towns over. Starting from the end of the left panel of Fig. 10.7, imagine that the two recently split packets keep going, then are both reflected back by mirrors. The beam splitter from the previous step has been removed. The blobs will approach each other in the vertical direction, cross each other (with interference), then continue on until their positions have been swapped and they look just like the final states of both panels in Fig. 10.7.
The sequence of manipulations discussed above is now summarized in Fig. 10.8. The question we are trying to answer is, what is the probability you should assign to your perception of one blob or another. In the initial state, we want to know the probability that you find yourself perceiving the high amplitude blob or the low amplitude blob. Let’s call the probability that you find yourself in the high amplitude blob \(A\), and the probability of the low amplitude blob \(B\), as labeled in the figure. Since the probabilities must sum to 1, \(B = 1 - A\).
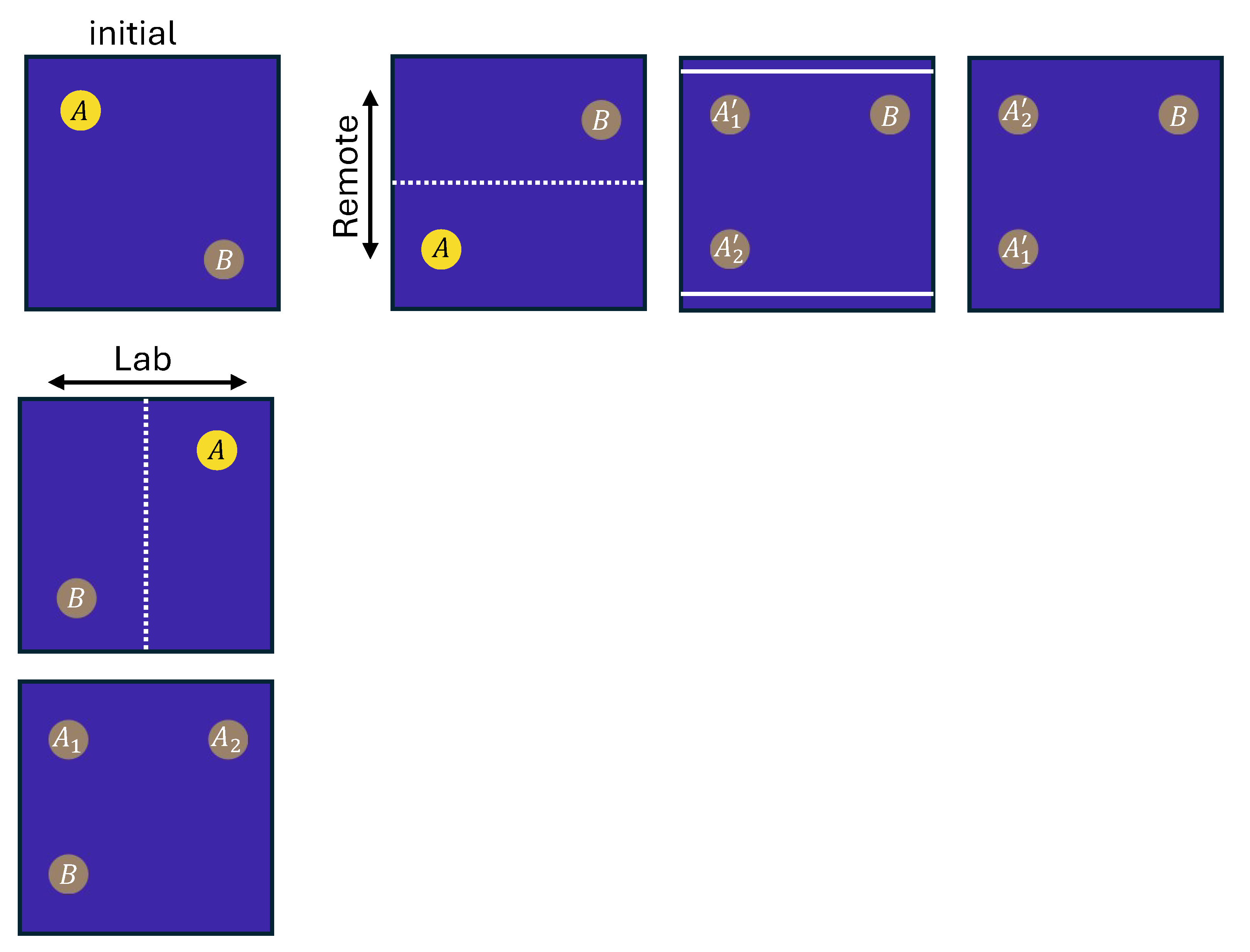
None of the remote manipulations can affect the probabilities we assign in the lab, since we have no way of knowing whether they have occurred or not. After the first remote swap, we still have probability \(A\) in the same spot on the left and probability \(B\) in the same spot on the right. The swapped position of the photon packets makes no difference to us in the lab.
Likewise, when the photon is then split, the probabilities in the lab must remain the same. Let’s say the probabilities of perceiving the two new blobs are \(A'_1\) and \(A'_2\), as labeled. The lower amplitude blob stays put, so the probability in that location remains \(B\). The probabilities must sum to 1, so we know that \(A = A'_1 + A'_2\).
The final swap at the right of Fig. 10.8 leaves the state unchanged, except the labels \(A'_1\) and \(A'_2\) are swapped. This means that \(A'_1 = A'_2= A/2\).
Now in the lab, the first swap interchanges the two blobs along the lab (horizontal) axis, so we would expect the probabilities of our perception in the lab to be swapped. Now probability \(A\) is on the right and \(B\) is on the left. After the split, at the bottom of Fig. 10.8, \(B\) has been left alone, while \(A\) has been split into \(A_1\) and \(A_2\). Now, since the state is exactly the same as the two rightmost panels in Fig. 10.8, we can equate the probabilities of the corresponding blobs. Without too much difficulty, we can see that all three blobs are equal: \(B = A_1 = A_2\). Since they must sum to 1, we know that they all equal 1/3.
Returning to our original question, we have determined that \(A = 2/3\) and \(B = 1/3\). Phew!
This has been a long explanation of how equal-shaped and equal-amplitude blobs have equal probability. This is maybe not too surprising. We can generalize this conclusion as follows:
Let’s say we start with an unequal superposition where the amplitudes squared are in the ratio \(m:n\), where \(m\) and \(n\) are integers. (If the actual ratio is irrational, we can approximate it arbitrarily well with a ratio of integers).
Upon measurement of this state, particles of the apparatus and/or environment become entangled with the particle being measured. This results in a state that looks like the beginning of Fig. 10.5.
To figure out the probabilities, we can divide up the two components of a remote entangled particle in the apparatus or environment. The component entangled with the first component of the original particle gets divided into \(m\) equal parts, and the other component gets divided into \(n\) equal parts. Note that this doesn’t actually have to happen, we just need to think about the fact that it could happen.
Dividing a packet into \(m\) equal parts means that the original amplitude squared will be evenly divided up amongst the \(m\) parts which each have amplitude squared smaller by a factor of \(m\). Once we have divided up both components as described in the previous step, then we will have \(m+n\) components, all with the same amplitude.
As we have illustrated in the simple cases above, we can then argue that we should assign the same probability to perceiving all of the equal-amplitude blobs. The argument rests on the idea that we can shuffle the blobs around into a number of different states that are all equivalent to each other.
Recalling that what we want is the probabilities of perceiving the two original blobs, we can then say that the probability of perceiving the first blob is \(m/(m+n)\), and the probability of perceiving the second blob is \(n/(m+n)\). This goes by the name of Born’s rule.
Even more generally, we could say that if two components of a wave function that correspond to two measurement outcomes have amplitudes squared in a ratio of \(m:n\), then the probabilities of perceiving those outcomes are in the same ratio.
This derivation of Born’s rule produces something that looks a little different from the usual statement of Born’s rule in the quantum measurement axiom, but it is really the same thing. In the usual version, there is a requirement imposed that all states must be “normalized” meaning that their amplitudes squared must sum (or integrate) to 1. This allows a slightly different statement of Born’s rule. However, we do not require the state to be normalized here. In fact, the explanation above is more clear if we do not assume a normalized state.
Finally getting back to our thrilling story. We have determined that Vinnie was wrong once again. He naively assumed that the probabilities would depend on the ratio of amplitudes (\(\sqrt{2}:1\)). We have determined that the probabilities actually depend on the ratio of amplitudes squared (\(2:1\)). Therefore, we can use our better understanding to place a bet that will, on average earn us a profit.
Now when the measurement is completed, there will be a happy version of you that has won the bet, and a sad version of you that has lost. But we perceive the happy outcome twice as often as the sad outcome. One way to understand this is to think of what would happen if the photon (unbeknownst to you) had split as shown in Fig. 10.5, resulting in three equal-amplitude blobs. Then you could imagine three versions of you: two happy and one sad with equal probability, each correlated with one of the equal-amplitude blobs.
We have now demonstrated how every prediction of the measurement axiom can occur without invoking the measurement axiom, save one. That one prediction is the “collapse” of the state upon measurement. This leads us to the conclusion that we do not require the measurement axiom at all if we accept that the state does not collapse, and that multiple measurement outcomes occur simultaneously as if they were separately occupying in Many Worlds.