Quantum waves

In quantum mechanics, the position and motion of a particle are represented by a wave. This wave is called a wave function. This is different than a classical wave on a string, which is made of a large number of particles, each with its own distinct displacement and velocity. A quantum wave function can represent just a single particle. The amplitude of the wave represents not a spatial displacement of something, but instead, in a sense, indicates the location of the particle. This is strange — a wave typically has amplitude spread across many locations. Indeed, this can be understood to mean that the particle has not just a single location, but is “in” many locations at the same time. This is the thing about quantum mechanics that is fundamentally different than classical mechanics, and we will see below how it leads to surprising and non-intuitive phenomena. One of the primary goals of this document is to clarify what is meant by this rather vague statement.

It turns out that we have already snuck in a preview of quantum waves, which are essentially just Klein-Gordon waves. [1] The Klein-Gordon equation describes particles in a way that includes the effects of special relativity. Notably, this includes the rest mass/energy of the particle according to \(E=mc^2\) and the fact that the momentum is not just proportional to the velocity, but a combination of the rest mass and velocity. The rest mass of the particle takes the place of the tennis net in the classical example above. This is a constant contribution to the energy that, regardless of the length of any waves, causes oscillations at the minimum frequency \(m\). Now we see that \(m\) is actually the mass of the particle. (Or in SI units, the minimum frequency is \(m c^2/\hbar\).) We will concern ourselves here with the non-relativistic limit — when the additional oscillations caused by waves are very slow compared to those caused by the rest mass. In this case, it makes sense to strip away the fast oscillations at \(m\), as was done above in the tennis net example. When we do that, we again obtain waves with two components that are typically combined together into a complex wave function \(\Psi\). [2] In this non-relativistic limit, we find that the Klein-Gordon equation reduces to the familiar equation of the non-relativistic quantum mechanics – the Schrödinger equation. [3]

Despite their differing interpretations, quantum waves still exhibit the same list of properties enumerated above for classical waves: propagation, reflection, superposition, interference, and interaction. Classical Klein-Gordon waves even exhibit properties such as tunneling that are sometimes viewed as particularly “quantum.” So what makes quantum mechanics so different from classical mechanics? One major difference arises when we want to describe more than one particle.

Just as a single particle is simultaneously located at multiple positions, a pair of particles are simultaneously located at multiple pairs of positions. That is the key idea. The wave function for two particles contains information about these pairs of positions.

A wave function describing two particles moving in one dimension must be written as \(\Psi(x_1,x_2,t)\). That is, it must tell us the amplitude for the two particles to be at every pair of positions \((x_1,x_2)\) over time. In comparison, two 1D classical waves \(d_1(x,t)\) and \(d_2(x,t)\) could be written this way as \(D(x_1,x_2,t) = d_1(x_1,t)\cdot d_2(x_2,t)\), but there was no particularly good reason to do so. On the other hand, a quantum 2-particle wave function \(\Psi(x_1,x_2,t)\) might be possible to split up into two waves \(\Psi_1(x,t)\) and \(\Psi_2(x,t)\) such that \(\Psi(x_1,x_2,t) = \Psi_1(x_1,t) \cdot \Psi_2(x_2,t)\), but in general this is not possible.

Let’s look at some examples. [4] In general, we will present examples of quantum waves in the form of wave packets. Recall that a “wave packet” refers to a spatially-localized pulse of waves, as has been shown in many of the examples above. Quantum waves, like classical waves, do not need to be localized in a packet. A quantum wave could be spread out over all of space. But waves in the form of packets make it easy for us to think about the classical picture of a particle, where the point-like particle exists at just one location.

First, at the left of Fig. 2.1, we look at a wave function where the first particle is located in the vicinity of position A, and the second particle is located in the vicinity of position C. Just like in the classical case, we can think of this as two separate 1D wave functions, or as a combined product of the two wave functions. It doesn’t make any difference. The 2D plot is mostly blue, representing zero amplitude of the wave function, with a yellow blob at the coordinates \((A, C)\), meaning a high amplitude for particle 1 to be near A and particle 2 to be near C.

Figure 2.1

Examples of non-entangled two-particle wave functions. 2D plots show where particles are located as yellow blobs, with the single particle wave functions shown below and to the right.

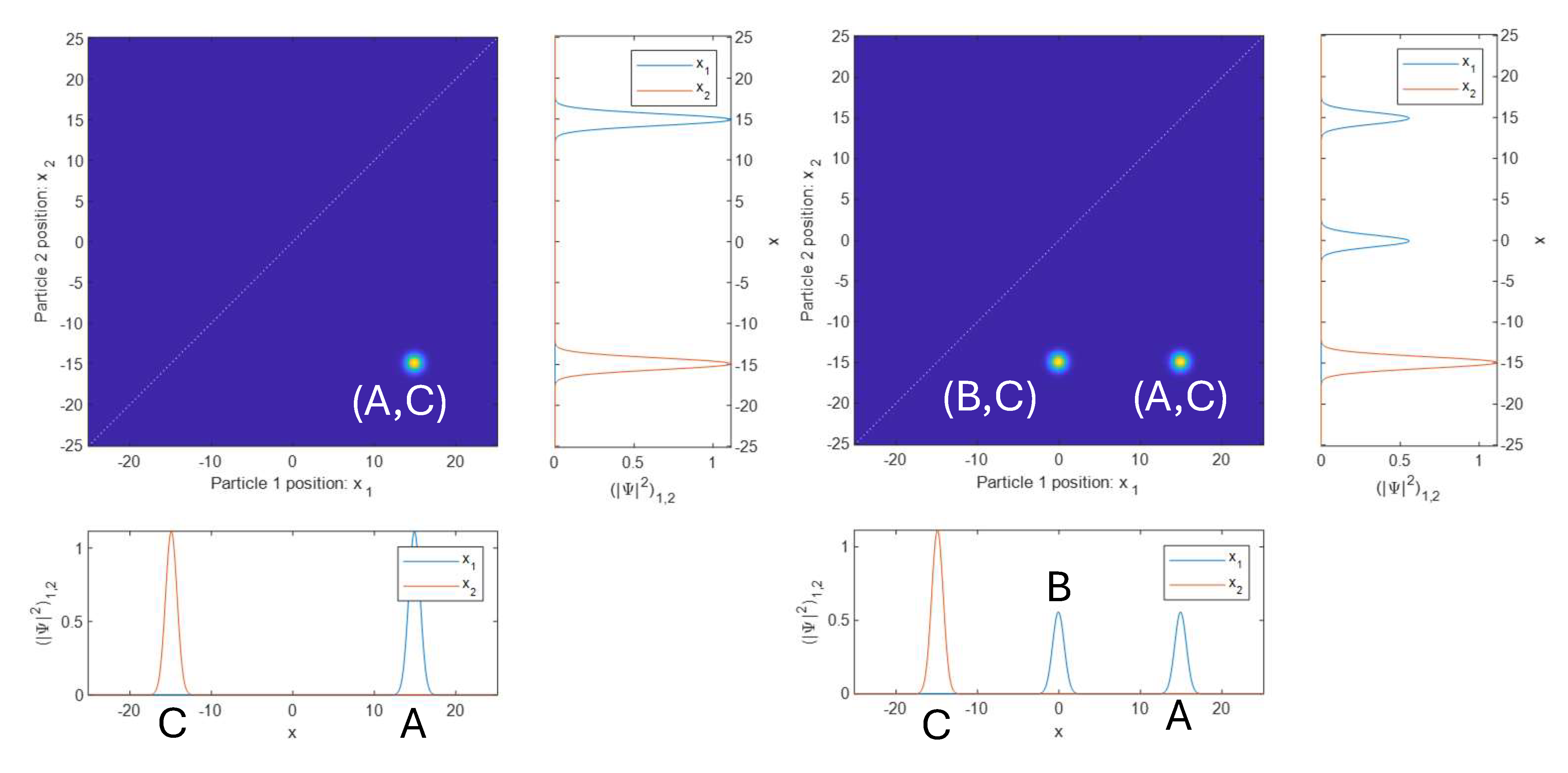
Since this state shown in Fig. 2.1 (left) is not entangled, we can also separately plot the wave function for both particles. This is shown twice in the figure, once below the horizontal axis, and once to the right of the vertical axis. Note that in the horizontal version of the 1D plot, the blue peak (particle 1) at A lines up with the yellow blob in the 2D plot, and that in the vertical version of the 1D plot, the red peak (particle 2) at C lines up with the yellow blob in the 2D plot. This highlights how the 2D plot should be interpreted.

It is important to keep in mind that we are describing two particles moving in one dimension only. The 2D plot can mistakenly look like we are showing particles on a 2D plane, but remember that the yellow blob is really telling us the location of two separate particles along a line. These types of plots will be used many times throughout, and they always represent some number of particles moving in one dimension. Later, we will see three particles moving in one dimension, which must be represented as a blob in three-dimensional space. Note that if we wanted to depict the state of two particles moving in two dimensions, i.e. on a plane, we would require a four-dimensional plot, which is already extremely difficult to visualize.

A slightly more complicated, though still not entangled, two-particle wave function is shown at the right of Fig. 2.1. Here, particle 1 is located both near positions A and B. Particle 2 is still located just near position C. Now the 2D plot shows two yellow blobs, representing the amplitude for the two particles to be near pairs of positions \((A,C)\) and \((B,C)\). Again, since the state is not entangled, we also plot the individual particle wave functions below and to the side of the 2D plot. In the bottom plot, we see that that the two peaks of the blue wave function (particle 1) at A and B line up with the two yellow blobs above. And in the side plot, the single peak of the red wave function (particle 2) at C lines up with the blobs, which are both at the same vertical position.

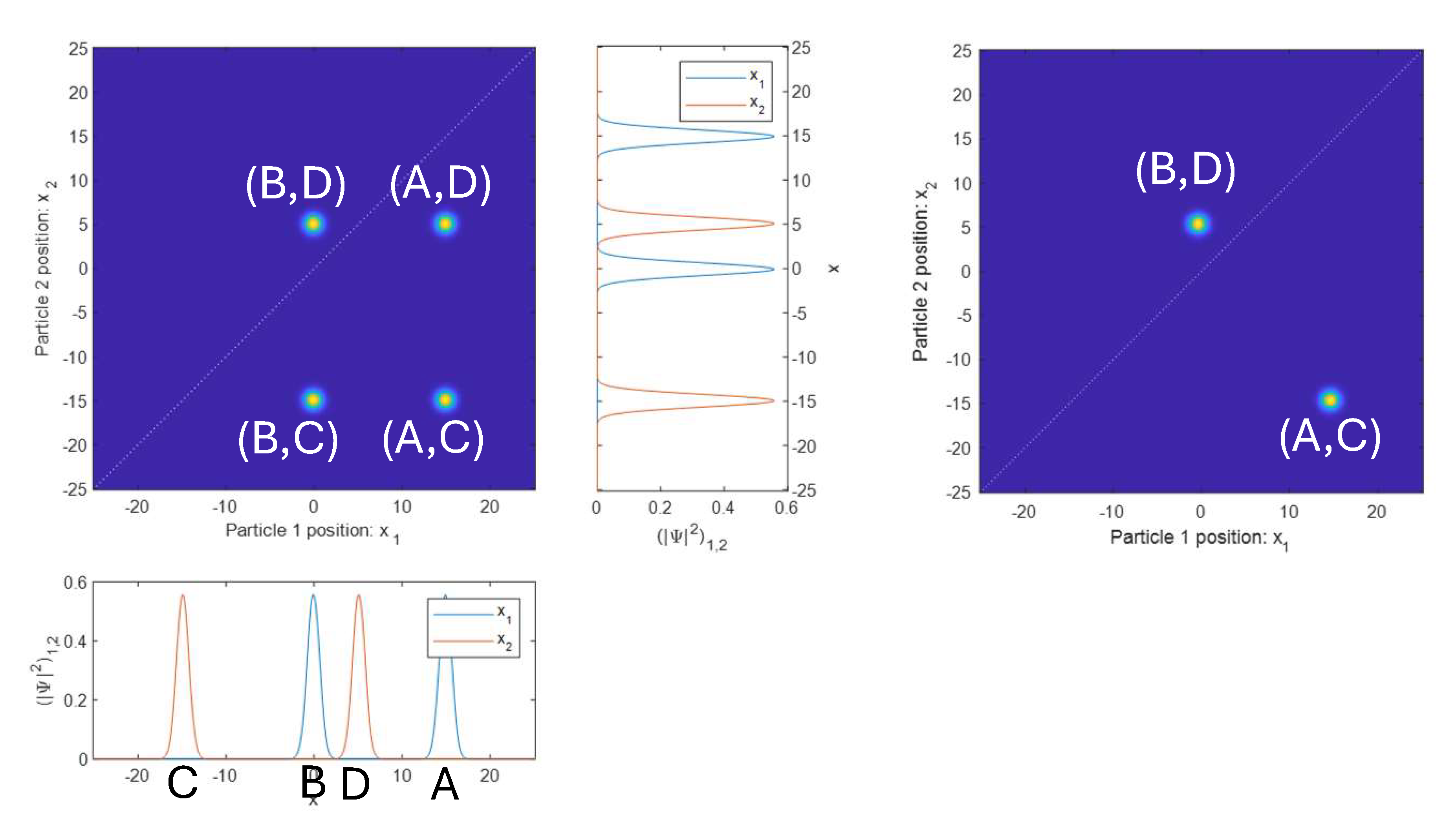
As a final example of two non-entangled particles, we now have both particles located near two different positions, shown at the left of Fig. 2.2. Particle 1 is near A and B, and particle 2 is near C and D. As such, we now have four yellow blobs, indicating amplitude for the particles to be at pairs of positions: \((A,C)\), \((B,C)\), \((A,D)\), and \((B,D)\). Plotting the single-particle wave functions separately, we again see how the peaks from the two particles line up with the yellow blobs in the horizontal and vertical directions.

Figure 2.2

Examples of two-particle wave functions - not entangled on the left, and entangled on the right. 2D plots show where particles are located as yellow blobs. Single-particle wave functions shown below and to the right. The entangled state cannot be decomposed into single-particle wave functions.

All of the two-particle wave functions shown so far are directly analogous to classical waves on two strings. We can wiggle a jump rope twice to make two wave packets, and do the same on another jump rope. We are then free to represent that pair of jump ropes by multiplying the waves together with separate x axes, and showing the results as a 2D plot. The result will look just like the left of Fig. 2.2.

At last, we will look at an example of a state that is entangled (Fig. 2.2, right). Now we see two yellow blobs, with amplitude at pairs of positions \((A,C)\) and \((B,D)\). That is, there is some amplitude for particle 1 and 2 to be located near positions A and C, respectively, and B and D, respectively. This has no analogue in the classical case. Such a state is called an “entangled” state.

You can probably see why the entangled two-particle wave function in Fig. 2.2 cannot be separated into two individual single-particle wave functions. In all of the non-entangled examples in Fig. 2.1 and Fig. 2.2 the yellow blobs must have replicas that line up with each other in the horizontal and vertical directions. This occurs because the two single particle wave functions would be multiplied together to make the two-particle wave function. Any position \(x_1\) where the particle 1 wave function is zero will be zero everywhere along the line of that \(x_1\) in the 2D plot. It can’t be zero at some peaks of the particle 2 wave function, and non-zero at others.

Entangled states of two or more particles can be confusing to understand. On the other hand, states are generally entangled. That is, non-entangled states are a rarely occurring simple case. So to understand the nature of the quantum world, we need to make an effort to understand entanglement.

Now that we have seen examples of entangled and non-entangled two-particle wave functions, we will look at some examples of how two-particle wave functions evolve in time.

First we look at an initial configuration similar to that shown at the left of Fig. 2.1. Figure Fig. 2.3 shows that particle 1 is initially located near a position at the right, and particle 2 is initially located near a position at the left. Since these particles are not entangled, we can plot the two single-particle wave functions separately, here in blue and red. The top panel shows the two components (real and imaginary) of the wave functions as solid and dotted lines. The lower panel shows the amplitude squared of the two wave functions. Particle 1, initially at the right, propagates to the left, while particle 2 starts at the left and propagates towards the right. There are several things to note in this example:

• The particle on the left has shorter waves than the particle on the right. The wavelength of the wave is inversely proportional to the momentum. So, since the two particles have the same mass, the particle starting on the left will move faster.

• The wave packets spread out over time. This is an unavoidable consequence of confining a wave into a packet. The same spreading was seen in the classical Klein-Gordon wave packets above. This spreading is a result of the Heisenberg uncertainty principle. Because the wave is localized in position, it cannot have a perfectly well-defined momentum. Instead it has a range of momentum, causing some fraction of the wave to go slower and some fraction to go faster, resulting in spreading.

• The two components (real and imaginary) oscillate, but the amplitude squared does not oscillate. It just translates, and spreads out.

Figure 2.3

Video example of two non-interacting, propagating wave packets plotted separately.

Figure 2.4 shows a similar two-particle situation, but plotted together in a 2D plot, where the horizontal axis shows the position of particle 1 and the vertical axis shows the position of particle 2. In this case, the two particles have the same momentum, but different mass – thus they move at different speeds. The two wave packets also start with a different widths. The color represents the amplitude squared. And just as in Fig. 2.1, we plot the amplitude squared for the two single-particle wave functions separately below and to the right. The wave packets of the two particles combine to form a single blob that moves in both the horizontal and vertical directions. The blob moves faster in the horizontal direction because the particle whose position is plotted on that axis is moving faster than the one corresponding to the vertical axis. The two particles move past each other when the blob passes through the dashed diagonal line. Nothing special happens here, because these particles do not interact with each other.

Figure 2.4

Video example of two non-interacting wave packets moving along a line plotted in 2D as a single two-particle wave function.

Now let’s take that previous example, but let the particles interact, either attracting or repelling each other. Charged particles like electrons and protons interact via their electric charge, with a potential energy that falls off proportional to the distance between them. Depending on whether that energy is positive or negative, the particles attract or repel. To make things easier to understand, we will take a different interaction potential that is zero when the particles are separated by more than some distance, and a constant value when they are closer than some distance. (A so-called ‘top-hat’ potential, from the appearance of a plot of the potential.) When we talk about the “distance” between the particles, we mean the distance between any pair of positions. The wave function tells us the amplitude for the two particles to be at any particular pair of positions. The distance between that pair of positions governs the potential seen by that part of the wave function. Examples below will serve to clarify this point.

For now, we take the same two particles as above, one starting on the left traveling right, and the other starting on the right traveling left (Fig. 2.5). The interaction is set so that at a distance greater than 1, the particles do not interact, and less than 1 they strongly repel each other. Initially, the particles move just as in the non-interacting case, because they are far enough apart that the interaction is zero. But when parts of the packets come within a distance of 1 from each other (or when the combined yellow blob comes within a distance of 1 from the dotted diagonal), then the two particles strongly repel and bounce off of each other. The reflection is similar to the reflection of a Klein-Gordon wave off of a fixed barrier shown above, but now the “barrier” is itself another particle.

Figure 2.5

Video example of two interacting wave packets moving along a line plotted in 2D as a single two-particle wave function. Positions separated by less than one unit of distance feel a repulsive interaction.

As a final example in this section, we will see how two interacting particles can start off not entangled, then become entangled (Fig. 2.6). All we have to do is to start one of the wave packets in a superposition of two distinctly different locations, then let the two particles interact. So we start in a configuration like the one shown in Fig. 2.1 on the right. Particle 1 is located near two positions, A and B towards the right side, and particle 2 is located near one position on the left. Then both parts of the particle 1 wave function start approaching particle 2. First the component of particle 1 that started near position B will begin to interact with particle 2, when it comes within a distance of 1 (or when the yellow blob nears the dotted diagonal.) Then just that one component of the wave function reflects, with the two components now traveling in opposite directions. At this point, the two-particle state is now entangled. The state is analogous to the one shown on the right of Fig. 2.2, with two blobs that are not aligned with each other in either the horizontal or vertical direction. There are now also two components to particle 2 – one that has collided with with particle 1 and one that hasn’t. Some time later, the second component of particle 1 collides with the second component of particle 2 and they also reflect off of each other. Now particle 1 and 2 are both moving in the opposite direction as they did initially, with two entangled components.

Figure 2.6

Video example of two interacting wave packets moving along a line plotted in 2D as a single two-particle wave function. The initial state is not entangled. After the interaction, the state is entangled.

In the next section, we will see how precisely this behavior two particles can be used to understand a classic puzzle of quantum mechanics – the double slit experiment.

Footnotes

[1]

A relativistic particle with mass and spin is more commonly represented using the Dirac equation, but the Dirac equation for a 4-component bispinor may be recast as a Klein-Gordon equation for a two-component spinor. See for example Feynman, R. P. and Gell-Mann, M., Phys. Rev. 109 (1958) 193.

[2]

In the quantum case, unlike the classical case, the Klein-Gordon wave also has two components most conveniently represented as real and imaginary parts, as well.

[3]

Actually, the complex Klein-Gordon equation reduces to two equations, a Schrödinger equation for particles, and a Schrödinger equation for antiparticles.

[4]

All multi-particle examples will be assumed to be composed of non-identical particles, e.g. an electron and a proton as opposed to two electrons. Identical particles require some additional subtleties that we prefer to avoid here for simplicity.